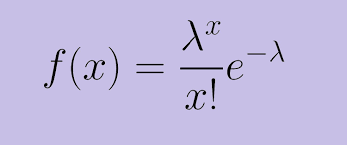In vele praktische voorbeelden hebben we te maken met een zeer groot aantal (n) onafhankelijke uitvoeringen van hetzelfde Bernoulli experiment, waarbij de succeskans (p) zeer klein is en waarbij het gemiddeld aantal successen ( np) ongeveer constant is. In dat geval kunnen de binomiale kansen vervangen worden door volgende functie: 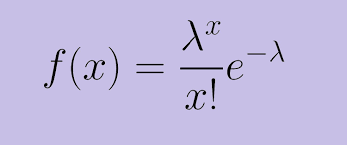
We zeggen dat X een Poissonverdeling heeft met parameter 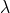 . De naam is ontleend aan de Franse wiskundige Siméon Poisson(1781-1840).
. De naam is ontleend aan de Franse wiskundige Siméon Poisson(1781-1840). 
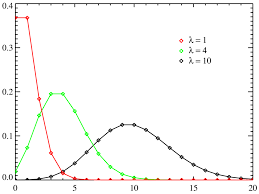
Er bestaan tabellen voor de Poissonverdeling. Het gemiddelde is 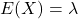 .
. 
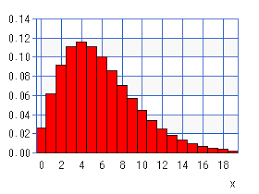
Een voorbeeld: Op 1 december ga ik voor mijn verjaardag naar een concert en bevind ik me in een zaal met 1000 personen. Noem X het aantal personen in de zaal die op dezelfde dag jarig zijn. Dan is X Poisson verdeeld met n=1000 en 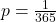 en dus
en dus 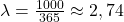
Dan is P(X=0)=0,06; P(X=1)=0,18; P(X=2)=0,24 ; P(X=3)=0,22; P(X=4)=0,15; P(X=5)=0,08
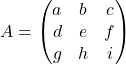 .
.![Rendered by QuickLaTeX.com \[det A =aei+bfg+dhc-gec-dbi-ahf\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-488f7b5bb7a20f5ecd7df36f05508736_l3.png)
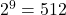 mogelijke matrices te vormen met nullen en enen.
mogelijke matrices te vormen met nullen en enen.![Rendered by QuickLaTeX.com \[\frac{168}{512}\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-d18444542bf1fa1c77aee68a871e8245_l3.png)