Een convexe zeshoek is ingeschreven in een cirkel met straal r. Twee zijden van deze zeshoek hebben als lengte 7 eenheden , terwijl de vier overige als lengte 20 eenheden hebben. Bepaal de straal van de cirkel.

Antwoord

Wat de volgorde van de zijden is, steeds moet minstens aan één zijde met lengte 7 een zijde met lengte 20 aanliggend zijn. Noem de middelpuntshoek tegenover de zijde met lengte 20 eenheden 2a en de middelpuntshoek tegenover de zijde met lengte 7 eenheden 2b.
Door het apothema te trekken op de zijden van de zeshoek vinden we dat 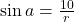$\sin a=\frac{10}{r}$ en $\sin b=\frac{3,5}{3}$ .
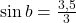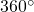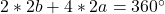De som van alle middelpuntshoeken is $360^\circ$ , dus $2*2b+4*2a=360^\circ$ . Hieruit volgt dat $b+2a=90^\circ$ .
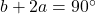Dan geldt er dat $\sin b=\cos 2a=1-2\sin^2 a$
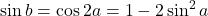
Volgens een vorig punt is dus 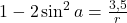$1-2\sin^2 a=\frac{3,5}{r}$ . Of
$1-2\Big(\frac{10}{r}\Big)^2=\frac{3,5}{r}$
Dit geeft een vierkantsvergelijking: $2r^2-7r-400=0$
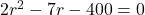
De enige positieve oplossing van deze vergelijking is 16.
De straal is 16 eenheden lang.