Gegeven is een cirkel met middelpunt A en straal R en een punt B buiten de cirkel. Neem een willekeurig punt Q op die cirkel en bereken het snijpunt P van QA met de middelloodlijn van QB. Bepaal de meetkundige plaats van de punten P als Q zich op d ecirkel beweegt.

We schakelen Geogebra in om een inpressie te krijgen van die meetkundige plaats:
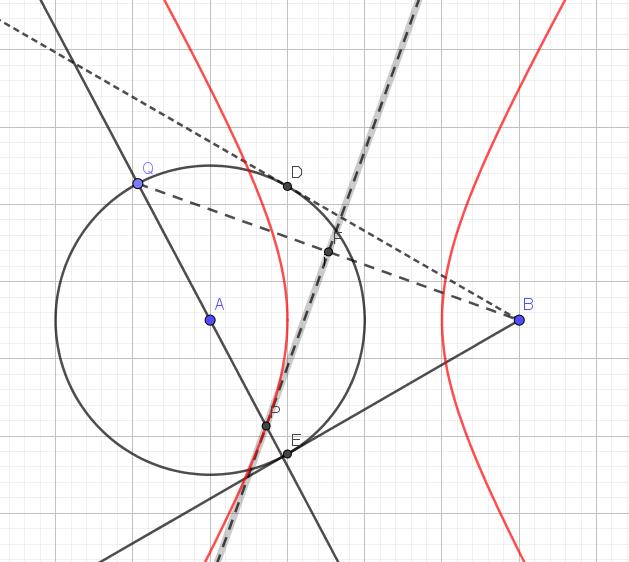
De oplossing lijkt een hyperbool te zijn. Omdat P op de middelloodlijn van QB ligt is 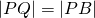$|PQ|=|PB|$ en bijgevolg is 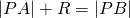$|PA|+R=|PB|$ of
$|PB|-|PA|=R$

Het verschil van de afstanden van P tot twee vaste punten A en B is dus constant en daarom is de meetkundige plaats inderdaad een hyperbool.
In de tekening zijn ook de raaklijnen uit B aan de cirkel getekent ( met raakpunten D en E). Als Q samenvalt met D of E dan bestaat P niet, omdat QA dan loodrecht staat op QB en dus evenwijdig is met de middelloodlijn.
Als Q samenvalt met de snijpunten van AB met de cirkel, dan vinden we de toppen van de hyperbool.
Als Q de grote boog DE doorloopt, dan vinden we de linkertak van de hyperbool. Het andere deel van de cirkel coorespondeert dan met de rechtertak.

Wiskunde is leuk