Tag archieven: meetkunde
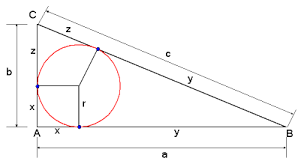
Straal ingeschreven cirkel
Zoek een verband tussen de zijden van een rechthoekige driehoek en de straal van de ingeschreven cirkel.
De stukken van de raaklijnen vanuit een punt aan de cirkel zijn even lang en bovendien is x = r.
Wanneer we ![]() berekenen vinden we dat
berekenen vinden we dat ![]() , dus geldt in een rechthoekige driehoek :
, dus geldt in een rechthoekige driehoek :
![]()
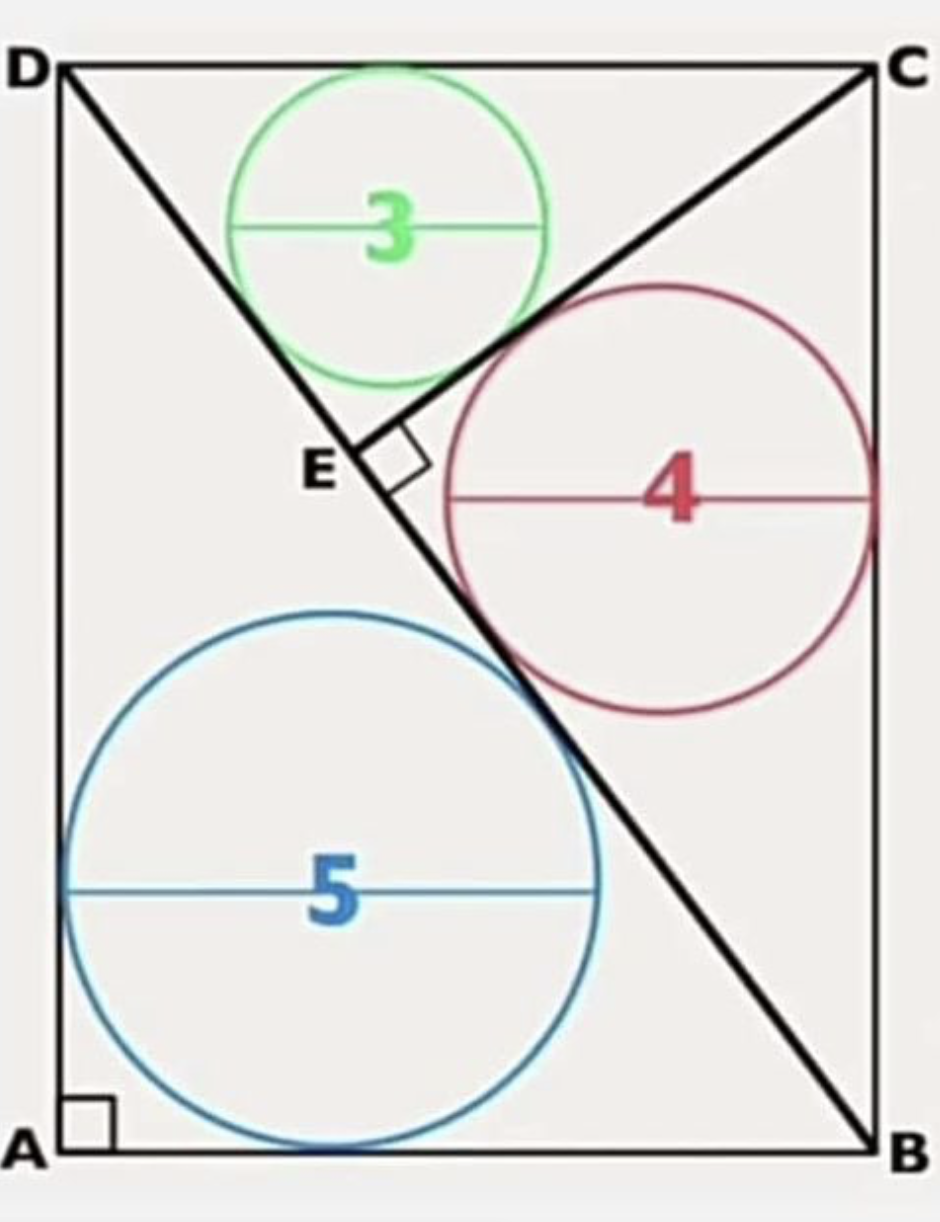
Kan je nu de oppervlakte van de rechthoek ABCD berekenen?
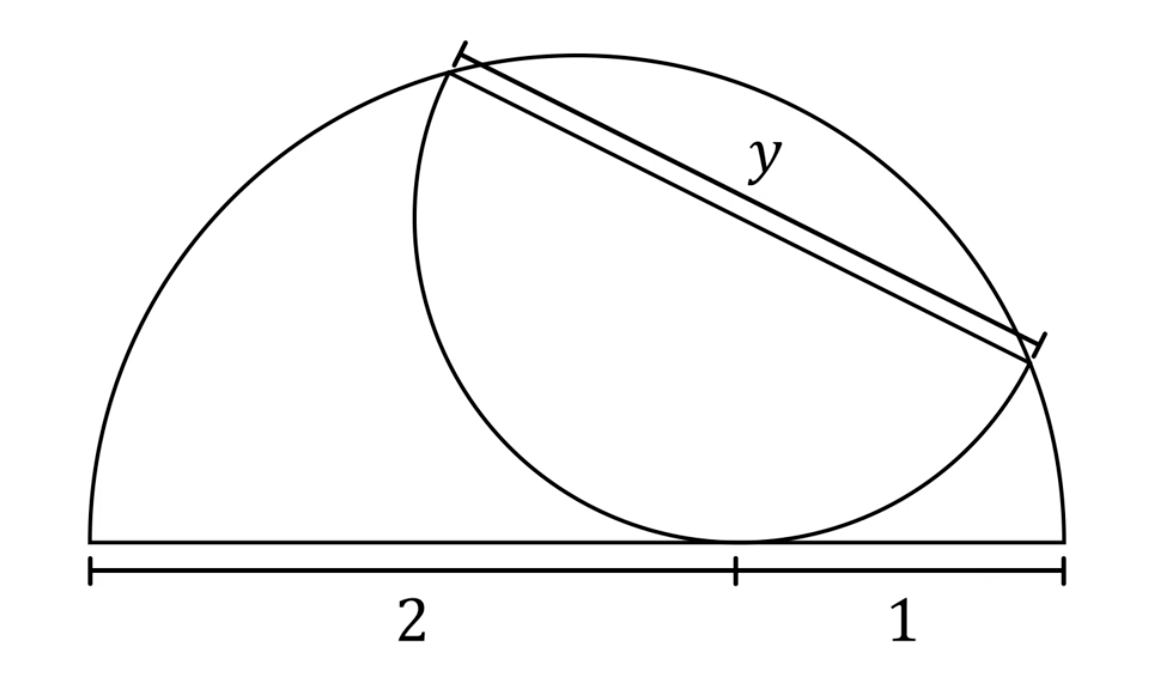
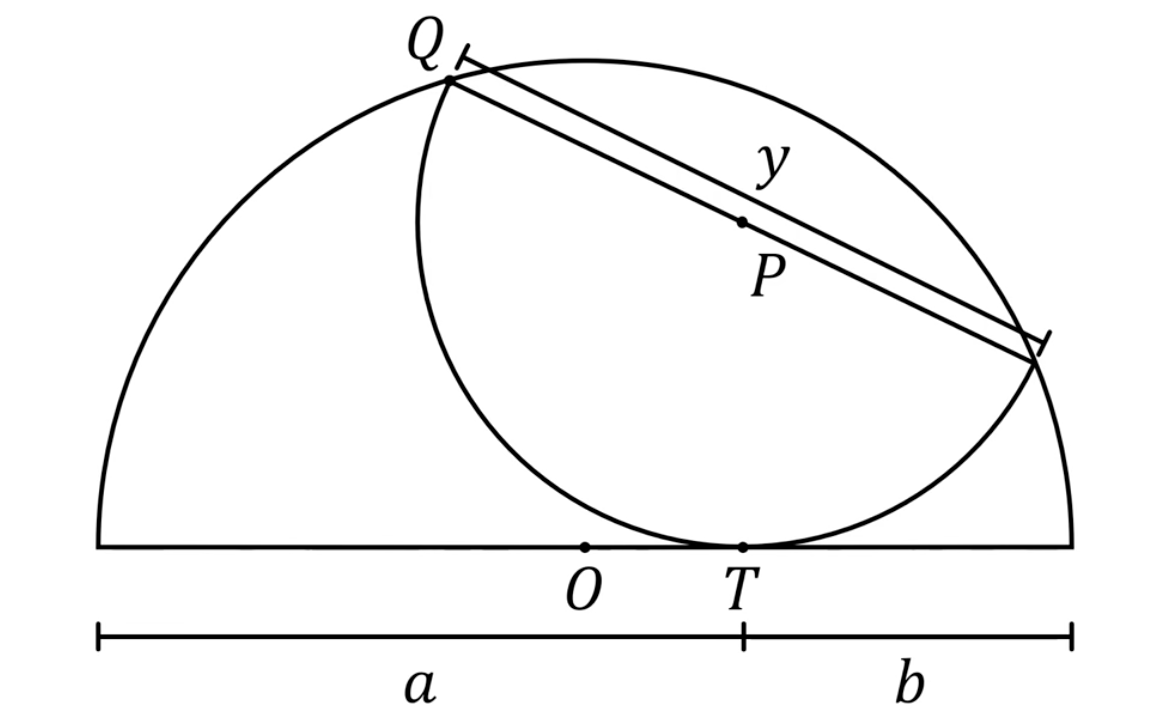
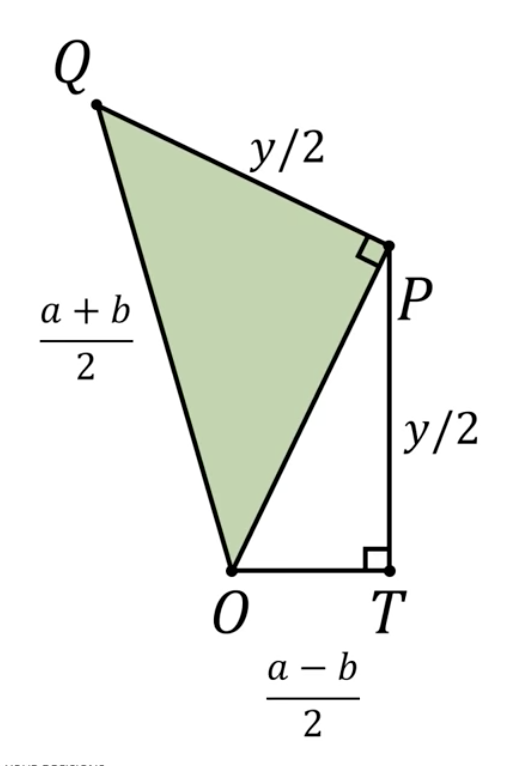
Nootje 25
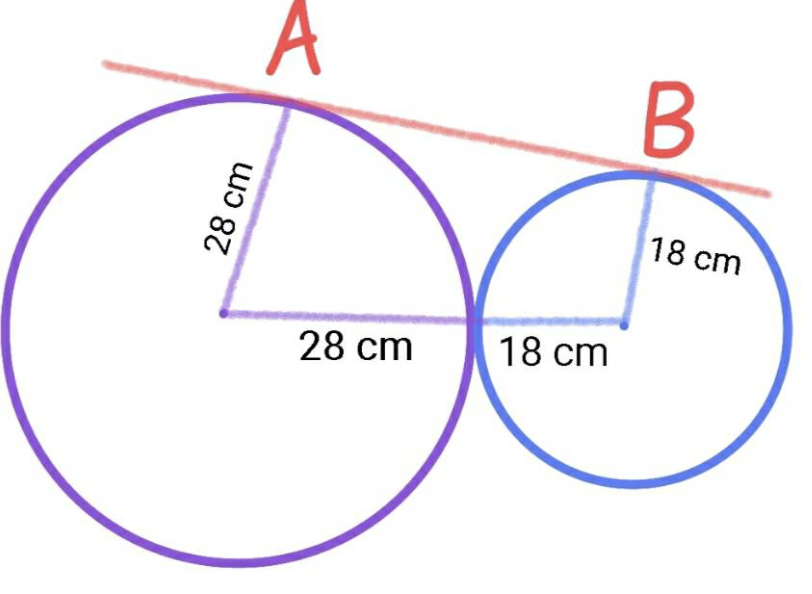
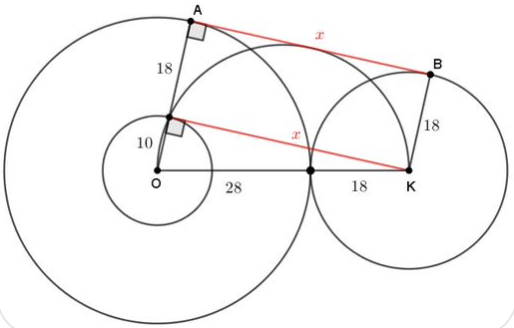
Bereken de lengte van de middellijn y.
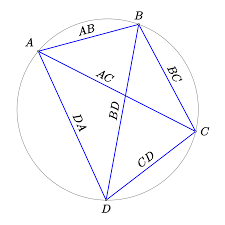
Stelling van Ptolemaeus
De kans, dat 4 willekeurig gekozen punten in het vlak, op 1 lijn of 1 cirkel liggen is erg klein. Er moeten dus wel speciale voorwaarden zijn om dit te doen gebeuren. Zo een voorwaarde wordt gegeven in de stelling van Ptolemaeus:
Voor 4 willekeurige punten A,B,C en D in het vlak, geldt ![]()
Enkele gevolgen:
- Als ABCD een koordenvierhoek is en ABC een gelijkzijdige driehoek, dan is
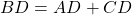 .
. - Als ABCD een koordenvierhoek is en de hoeken in B en D zijn recht, dan is
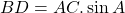 ( schrijf de hoek A als som van twee hoeken en pas de domformule voor
( schrijf de hoek A als som van twee hoeken en pas de domformule voor 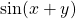 toe)
toe)
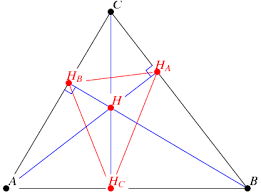
Hoogtedriehoek
De hoogtedriehoek van een driehoek ABC is de driehoek gevormd door de voetpunten van de drie hoogtelijnen van deze driehoek.
Enkele speciale eigenschappen:
- Het hoogtepunt van driehoek ABC is het middelpunt van de ingeschreven cirkel van zijn hoogtedriehoek.
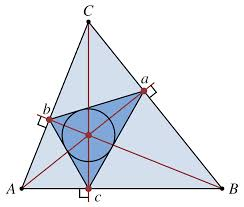
- Van alle driehoeken ingeschreven in driehoek ABC(d.i de hoekpunten liggen op de zijden van driehoek ABC) heeft de hoogtedriehoek de kleinste omtrek.
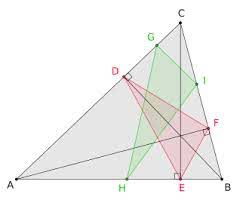 Dit wordt ook wel eens het probleem van Fagnano genoemd naar Giovanni Fagnano die dit probleem stelde in 1775.
Dit wordt ook wel eens het probleem van Fagnano genoemd naar Giovanni Fagnano die dit probleem stelde in 1775.