Bewijs dat er tussen elke 9 getallen er twee zijn, een a en een b, waarvoor
![]()
Antwoord
- De middelste uitdrukking doet me onmiddellijk denken aan de formule voor
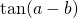 .
. - Bovendien volgt uit
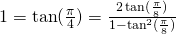 dat
dat 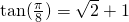 .
. - Verdeel nu het interval
![Rendered by QuickLaTeX.com ]-\frac{\pi}{2},\frac{\pi}{2}[](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-773949698f1462f506f7dfc63b7aaa9e_l3.png) in 8 gelijke stukken.
in 8 gelijke stukken. - Noteer de 9 gegeven getallen door
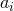 met
met 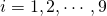 . Stel vervolgens
. Stel vervolgens 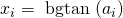 .
. - Er zijn 9 getallen
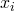 voor 8 intervallen, dus volgt uit het duivenhok principe dat er minstens twee getallen
voor 8 intervallen, dus volgt uit het duivenhok principe dat er minstens twee getallen 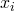 en
en 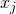 met
met 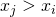 in hetzelfde interval liggen.
in hetzelfde interval liggen. - Dan geldt
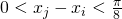 .
. - Omdat de tangensfunctie stijgend is op
![Rendered by QuickLaTeX.com ]-\frac{\pi}{2},\frac{\pi}{2}[](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-773949698f1462f506f7dfc63b7aaa9e_l3.png) , volgt hieruit dat
, volgt hieruit dat 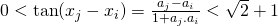 .
.
