Antwoord
- Noem deze uitdrukking x.
- Dan is
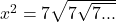 of
of 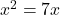 ;
; - Bijgevolg is
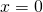 of
of 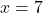 . Uiteraard kan 0 geen oplossing zijn, dus
. Uiteraard kan 0 geen oplossing zijn, dus 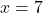 .
.

Stel ![]() en
en ![]() voor
voor ![]() Bereken dan
Bereken dan
![]()
Het is onwaarschijnlijk dat je alle functies ![]() , waarbij n varieert van 1 tot n, zal moeten berekenen. Waarschijnlijk zit er ergens een patroon in…
, waarbij n varieert van 1 tot n, zal moeten berekenen. Waarschijnlijk zit er ergens een patroon in…
![]()
![]()