Controleer voor elk natuurlijk getal vanaf 7 of 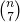${n} \choose {7}$ deelbaar is door 12 en bereken de fractie van dergelijke getallen. Zoek de limiet van die fractie als je steeds meer getallen controleert.

Antwoord

We weten dat ${n} \choose {7}$ = $\dfrac{n!}{7!(n-7)!}=\dfrac{n(n-1)\cdots(n-6)}{2^4.3^2.5.7}$
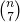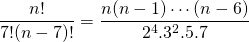
Om deelbaar te zijn door 12 moet de teller deelbaar zijn door 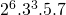${2^6.3^3.5.7}$ . Omdat de teller betsaat uit zeven opeenvolgende getallen is die zeker al deelbaar door 7 en 5.
Bekijken we nu de factoren 3. De teller is zeker deelbaar door 9, want zeven opeenvolgende getallen bevatten zeker twee veelvouden van 3.
Als 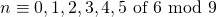$n \equiv 0,1,2,3,4,5 \text{ of } 6 \text{ mod } 9$ , dan is zeker één van de zeven getallen uit de teller deelbaar door 9 en een ander door 3, zodat de teller deelbaar is door $3^3$ .
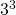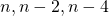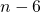Nu de factoren 2: Als n even is dan zijn $n,n-2,n-4$ en $n-6$ allemaal deelbaar door 2 en juist twee getallen zijn een viervoud, zodat de teller dan deelbaar is door $2^6$ .
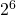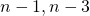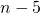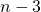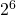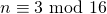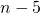Als n oneven is dan zijn $n-1,n-3$ en $n-5$ deelbaar door 2. Als $n-3$ het enige getal is dat deelbaar is door 4, dan moet het zelfs deelbaar zijn door 16 anders kan de teller niet deelbaar zijn door $2^6$ . Dus moet $n \equiv 3 \text{ mod } 16$ . Als $n-1$ en $n-5$ beiden deelbaar zijn door 4, dan moet opdat de teller deelbaar zou zijn door 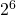$2^6$ , een van die getallen deelbaar zijn door 8. Dus moet 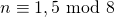$n \equiv 1,5 \text{ mod } 8$ of $n \equiv 1,5,9,13 \text{ mod } 16$ .
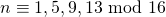Brengen we nu alle informatie samen: 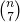${n} \choose {7}$ is deelbaar door 12 als en slechts als
$\begin{cases} n \equiv 0,1,2,3,4,5,6 \text{ mod } 9 \\ n \equiv 0,1,2,3,4,5,6 ,8,9,10,12,13,14 \text{ mod } 16$
Er zijn 7 mogelijkheden modulo 9 en 13 mogelijkheden modulo 16, dus zijn er volgens de Chinese reststelling 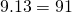$9.13=91$ oplossingen modulo $9.16=144$ .
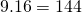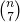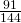De waarschijnlijkheid dat ${n} \choose {7}$ deelbaar is door 12 nadert dus de waarde $\frac{91}{144}$ .