Tag archieven: oppervlakte vierhoek

Oppervlakte vierhoek

Geplaatst op door

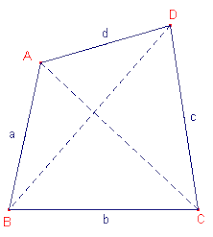
Welke convexe vierhoek, met vaste zijden a,b,c en d heeft de grootste oppervlakte?

  • Stel S de oppervlakte van de vierhoek ABCD. Gebruik de formule voor de oppervlakte van een driehoek: de helft van het product van twee zijden en de sinus van de ingesloten hoek : 2S=ab \sin B+cd \sin d.
  • We kunnen de diagonaal AC bepalen via de cosinusregel in de driehoeken ABC en ADC: |AC|^2=a^2+b^2-2ab\cos B=c^2+d^2-2cd\cos D.
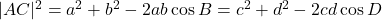  • Uit de laatste betrekking volgt dat

        \[\frac{1}{2}(a^2+b^2-c^2-d^2)=ab\cos B-cd \cos D\]

  • Kwadrateren  en optellen van de eerste formule en de laatste geeft:

        \[4S^2=a^2b^2+c^2d^2-2abcd\cos(B+D)-\frac{1}{4}(a^2+b^2-c^2-d^2)^2\]

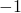  • Nu is S maximaal als \cos (B+D) minimaal is, dus gelijk aan -1. Maar dan zijn de hoeken B en D supplementair en is de vierhoek een koordenvierhoek en kan dus ingeschreven worden in een cirkel.
  • Als we deze waarde 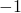-1 invullen in de vorige formule en we stellen a+b+c+d=2P, dan kunnen we hieruit die maximale oppervlakte bepalen:

        \[S=\sqrt{(P-a)(P-b)(P-c)(P-d)}\]

  • Deze formule is een veralgemening van de formule van Heroon voor een driehoek (stel d=0).