Het dartbord is in 1896 ontworpen door Brian Gamlin. 
De nummers werden zo geplaatst dat elk hoog getal tussen twee lage getallen ligt. Hoe groter het getal waarop je mikt, hoe meer je gestraft wordt als de pijl er net niet ingaat. Wie op de sector met getal 20 mikt, maar net mist, moet het doen met 1 of 5 punten.
Een mogelijk onderzoeksvraag zou kunnen zijn: kan je het bord ‘moeilijker’ maken? Er zijn immer heel veel borden mogelijk: we kunnen 20 getallen op 19! mogelijkheden rangschikken op een cirkel. Bij benadering zijn dat ongeveer 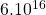 rangschikkingen. Hoe kunnen we de getallen dan rangschikken zodanig dat de grootste som van de trio’s zo klein mogelijk is en de kleinste som zo groot mogelijk? Op het gebruikelijke dart bord is de maximale som 42 en de minimale som 26. Er bestaat een schikking met maximale som 33 en minimale som 30.
rangschikkingen. Hoe kunnen we de getallen dan rangschikken zodanig dat de grootste som van de trio’s zo klein mogelijk is en de kleinste som zo groot mogelijk? Op het gebruikelijke dart bord is de maximale som 42 en de minimale som 26. Er bestaat een schikking met maximale som 33 en minimale som 30.

Een ander mogelijk onderzoek peilt waarnaar je het best kan richten om gemiddeld de hoogste score te halen. Wie niet zo goed kan darten kan beter niet op de 20 mikken omdat het risico in de 1 of 5 terecht te komen te groot is. Maar waar kan je dan wel het best op spelen? Op 7 lijkt een goed idee, want die heeft 2 hoge buren: 16 en 19. Als we aannemen dat een beginnende speler toch wel een beetje kan mikken, en dus ofwel de bedoelde sector ofwel één van zijn naaste buren zal raken, heeft het zin om dergelijke trio’s van sectoren te bekijken. We bestuderen twee gevallen:
- Stel dat elke sector van het trio dezelfde trefkans heeft. Wie op de 7 mikt heeft dan gemiddeld
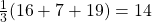 punten. Wie op de 20 mikt , gemiddeld slechts
punten. Wie op de 20 mikt , gemiddeld slechts 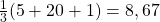 punten. Hier kan je dus beter op de 7 gaan spelen!
punten. Hier kan je dus beter op de 7 gaan spelen!
- Stel dat de trefkans ( kans om de sector waarop je mikt, ook te raken) gelijk is aan p en dat de kans om de twee buren te raken even groot is. dan is de trefkans van elk van de buren gelijk aan
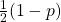 . De verwachte waarde voor het trio a,b,c is dan
. De verwachte waarde voor het trio a,b,c is dan 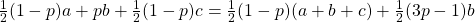 De verwachtingwaarde wordt dus bepaald door de som van het trio plus een term die afhangt van het middelste getal b en de kans p dat je die raakt? Voor p=0,6 is de verwachtingswaarde voor b=19 gelijk aan 13,4 en die van 20 is 13,2. De verwachtingswaarde voor b=7 is slechts 8. Onder deze voorwaarden kan je dus beter op de 19 mikken.
De verwachtingwaarde wordt dus bepaald door de som van het trio plus een term die afhangt van het middelste getal b en de kans p dat je die raakt? Voor p=0,6 is de verwachtingswaarde voor b=19 gelijk aan 13,4 en die van 20 is 13,2. De verwachtingswaarde voor b=7 is slechts 8. Onder deze voorwaarden kan je dus beter op de 19 mikken.






![Rendered by QuickLaTeX.com \[\begin{array}{c|c|c|c|c|c|c} A&3&1&2&0&3-1&4 \text{pt}\\B&3&1&2&0&4-3&4 \text{pt}\\C&3&0&3&0&2-2&3 \text{pt}\\D&3&0&1&2&0-3&1 \text{pt} \end{array}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-9ea3b031b3894a7fc932d589f4bd9de0_l3.png?media=1678572382)