Als de omtrek van een driehoek gelijk is aan 2, bewijs dan dat niet alle hoogtelijnen langer kunnen zijn dan 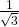 .
.
- Noteer de drie zijden van de driehoek door
 en
en  en de hoogtelijnen door
en de hoogtelijnen door 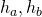 en
en 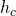 .
. - Er moet dus minstens 1 hoogtelijn kleiner zijn dan
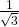 . De kleinste hoogtelijn staat loodrecht op de grootste zijde.
. De kleinste hoogtelijn staat loodrecht op de grootste zijde. - Veronderstel dat
 de grootste zijde is dan is
de grootste zijde is dan is  .
. - De oppervlakte van de driehoek is gelijk aan
 , maar ook gelijk aan
, maar ook gelijk aan 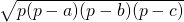 . Hierin is
. Hierin is 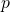 de halve omtrek en dus is
de halve omtrek en dus is  .
. - Bijgevolg is
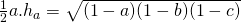 of
of 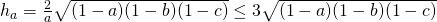 .
. - Gebruik nu de ongelijkheid van het meetkundig en rekenkundig gemiddelde :
![Rendered by QuickLaTeX.com \sqrt[3]{(1-a)(1-b)(1-c)}\leq \frac{1}{3}(1-a+1-b+1-c)=\frac{1}{3}](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-b17fe4eb9e5f4114d054e3acf4ffc34f_l3.png?media=1678572382) .
. - Hieruit volgt dat
 .
. - Ten slotte is dus
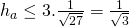 .
.