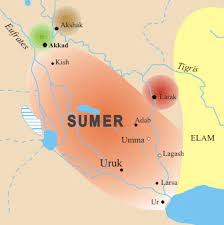
Derdegraads vergelijkingen: vervolg.

Geplaatst op 30 september 2022 door admin

In een vorig artikel hebben we de formules van Cardano besproken voor het oplossen van een willekeurige vergelijking van graad 3. Maar wat heeft de symmetrische groep van orde 6, $S_3$ hier mee te maken? En wat is de discriminant van zo een vergelijking? Is dat dan een veralgemening van de discriminant van een vergelijking van graad 2? Wil je hierover meer weten , lees dat dit vervolgartikel.

Opgave 36

Geplaatst op 26 september 2022 door admin

Wanneer deelt een natuurlijk getal n de uitdrukking $10^k-1$ voor een natuurlijke k?

Spoiler

Als n een veelvoud is van 2 of 5, dan is de enige mogelijkheid de triviale oplossing k=0.
Veronderstel dus verder dat n geen priemfactor 2 of 5 bevat.
Noteer met K(n) de kleinste, van 0 verschillende waarde van k, waarvoor $n|(10^k-1)$ .
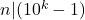Proberen we een aantal waarden uit:
$\begin{array}{c|c} n&K(n) \\ \hline \\ 3&1\\7&6\\9&1\\11&2 \end{array}$
Stel nu dat n, geen priemfactor 2 of 5 bevat, en een deler is van 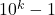$10^k-1$ , dan bestaat er een natuurlijk getal a zodat $n.a=10^k-1$ .
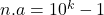Noteer de decimale schrijfwijze van a als $a=a_110^{k-1}+\cdots+a_{k-1}10+a_k$ .
Dan is $a_110^{k-1}+\cdots+a_{k-1}10+a_k=\frac{10^k}{n}-\frac{1}{n}$ .
Bij deling, van deze laatste vergelijking door 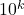$10^k$ vinden we:
$0,a_1\cdots a_{k-1}a_k=\frac{1}{n}-\frac{10^{-k}}{n}$
Als we steeds maar opnieuw delen door 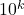$10^k$ en alle bekomen formules lid per lid bij elkaar optellen vinden we
$\frac{1}{n}=0,a_1\cdots a_{k-1}a_ka_1\cdots a_{k-1}a_k\cdots$
Omgekeerd is het eenvoudig te zien dat, als $\frac{1}{n}$ een decimale ontwikkeling zoals hierboven heeft, dat n een deler is van 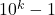$10^k-1$ .
Besluit: Als n geen priemfactor 2 of 5 bevat, dan in K(n) gelijk aan de lengte van de periode van $\frac{1}{n}$ .
Natuurlijk is elk veelvoud van k ook een goede oplossing.

Uruk en de eerste steden (3750-3150 v.C.)

Geplaatst op 19 september 2022 door admin

Uruk wordt beschouwd als de eerste echte stad De stad lag te midden van moerassen waar volop vis en gevogelte te vangen was. In de loop van het vierde millennium was er een grote bevolkingstoename. De toenemende bedrijvigheid trok mensen uit de wijde omgeving aan en op zijn hoogtepunt telde Uruk ongeveer 40000 inwoners.

Om vreedzaam te kunnen samenleven groeide de behoefde aan een gemeenschappelijke identiteit, niet gebaseerd op familieverwantschap, maar op het inwonerschap van de stad. Daarvoor was een symbool nodig waar iedereen belang aan hechtte: de hemelgod Anu eb de vruchtbaarheidsgodin Inanna werden verheven tot beschermgoden van de stad.

Om te bemiddelen tussen de goden en de inwoners van Uruk werd 1 man aangesteld als priester-koning. Om de tempelgebouwen te onderhouden en de offerceremoniën te leiden, ontstond een instelling: ‘de tempel’. Dit instituut kon van de inwoners eisen dat ze een deel van hun oogsten afstonden. De tempel bezat bovendien een groot deel van de landbouwgrond rond de stad en had veel mensen in dienst. Om de administratie hiervan in goede banen te leiden werd het schrift ontwikkeld en kwam een bureaucratie tot stand.

In de loop van het vierde millennium bleef de tempel de enige werkelijke autoriteit binnen de stadstaat. De sociale en economische verschillen tussen de inwoners waren eerder klein.

Uruk was niet uniek. Tegelijkertijd ontstonden ook andere dichtbevolkte en economisch dynamische steden: Eridu, Nippur,Ur,Lagash, Umma,…

Wie waren de inwoners van deze steden? Het Soemerische volk: een nieuwe bevolkingsgroep die bij aankomst in Mesopotamië de sociale, culturele en technische veranderingen van deze Uruk periode mogelijk maakte of een volk dat al lang ( 5000 v.C.) in Zuid-Mesopotamië woonde?

Opgave 35

Geplaatst op 14 september 2022 door admin

N is een natuurlijk getal. Een goede verdeling van N is een partitie van $\{1,2,\cdots,N\}$ in twee gescheiden, niet lege deelverzamelingen $S_1$ en $S_2$ , zo dat de som van de elementen van $S_1$ gelijk is aan het product van de elementen van $S_2$ . Bewijs dat voor $N\geq 5$ er altijd een goede verdeling bestaat.

Spoiler

Laten we eerst even op verkenning gaan en kijken of we een goede verdeling vinden voor 5,6 en 7.
Voor 5 vinden we $S_1=\{3,5\}$ en $S_2=\{1,2,4\}$ .
Voor 6 vinden we 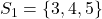$S_1=\{3,4,5\}$ en $S_2=\{1,2,6\}$ .
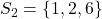Voor 7 vinden we $S_1=\{2,4,5,7\}$ en $S_2=\{1,3,6\}$ .
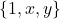In deze voorbeelden vinden we $S_21$ van de vorm $\{1,x,y\}$ . Proberen we eens of dit altijd kan!
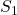$S_1$ is het complement van $S_2$ dus we krijgen een goede verdeling als
$\frac{N(N+1)}{2}-1-x-y=xy$
Uitgewerkt geeft dit $(x+1)(y+1)=\frac{N(N+1)}{2}$ .
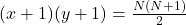Als nu $N\geq 5$ en N even is , dan kunnen we voor x en y volgende oplossingen vinden:
$x=\frac{N}{2}-1 \text{ en } y=N$
Als N echter oneven is, vinden we:
$x=\frac{N+1}{2}-1 \text{ en } y=N-1$
We hebben dus een constructie bewijs gegeven van het gevraagde.

Grazende koeien

Geplaatst op 9 september 2022 door admin

Op een weide grazen 70 koeien in 24 dagen de hele weide kaal. Zou men er slechts 30 koeien opzetten dan was er voldoende gras voor 60 dagen. Hoeveel koeien kan men op de weide plaatsen als men wilt dat er voldoende voedsel is voor 96 dagen?

Hoe meer koeien hoe minder graasdagen? Dus omgekeerd evenredig?
Neen, want dan zou het product van het aantal koeien en het aantal graasdagen constant moeten zijn en in ons verhaal is dat niet zo :
$70*24\neq 30*60$
Er zit een verborgen onbekende in ons probleem. We mogen gerust veronderstellen dat het gras op gelijkmatige wijze groeit van dag tot dag. Noteer met y de dagelijkse aangroei van de grashoeveelheid als fractie van de oorspronkelijke hoeveelheid. Stel de oorspronkelijke hoeveelheid gras door door 1.
Per dag eten de koeien dan, in het eerste geval,
$\frac{1+24y}{24}$
Per koe en per dag is dat dan
$\frac{1+24y}{24*70}$
Een analoge redenering voor de tweede situatie geeft dan:
$\frac{1+60y}{30*60}$
Door deze 2 formules aan elkaar gelijk te stellen vinden we $y=\frac{1}{480}$
Elke koe eet dus per dag een $\frac{1}{1600}$ -ste deel van de oorspronkelijke hoeveelheid gras eet.
In te vullen in het laatste gegeven, waarbij we het aantal koeien voorstellen door x, krijgen we :
$\frac{1+96\frac{1}{480}}{96x}=\frac{1}{1600}$
Hieruit volgt dat $x=20$ .