Dames in een kaartspel

Geplaatst op 29 maart 2024 door admin

Schud een spel kaarten goed. Hoeveel kaarten van de top , gemiddeld genomen, kom je de eerste dame tegen?

We weten dat er 4 dames in het spel zijn.
Wat ook de volgorde van de kaarten mag zijn, de dames verdelen het pak kaarten in 5 groepen: de kaarten voor de eerste dame, de kaarten tussen de eerste en tweede dame, enzovoort.
Het aantal kaarten in elk van die groepen varieert van 0 tot en met 48.
Noteer met 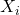$X_i$ het aantal kaarten in de i-de groep. Dan geldt:
$0 \leq X_i \leq 48$

$X_1+X_2+X_3+X_4+X_5=48$
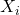Elke $X_i$ is een kansvariabele en omdat het pak kaarten goed geschud is, zal de kansverdeling van elke 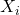$X_i$ dezelfde zijn.
Maar dan is $48=E(48)=E(X_1+X_2+X_3+X_4+X_5)=5E(X_1)$ .
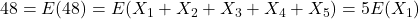Bijgevolg is
$E(X_1)=\frac{48}{5}=9,6$
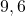Het verwacht aantal kaarten voor de eerste dame is dus gelijk aan $9,6$ .

Geplaatst op 26 maart 2024 door admin

Gegeven een matrix $A=\begin{pmatrix}a&b&c\\d&e&f\\g&h&i\end{pmatrix}$ .
Zijn determinant is
$det A =aei+bfg+dhc-gec-dbi-ahf$
Omdat het gaat over even/oneven kunnen we modulo 2 werken.
Determinant oneven betekent dan dat de determinant 1 is en dus dat de matrix inverteerbaar moet zijn.
Een matrix is inverteerbaar als de kolommen onafhankelijk zijn. Kies de eerste kolom willekeurig ( mag niet 000 zijn) . Dan heb je hiervoor 7 mogelijkheden.
De tweede kolom mag geen veelvoud zijn van de eerste, maw mag er niet aan gelijk zijn. Dus heb je hiervoor nog 6 mogelijkheden.
De derde kolom mag niet gelijk zijn aan de eerset of de tweede , maar ook niet gelijk aan de som van die twee ( en natuurlijk ook niet 000). Hiervoor heb je 4 mogelijkheden .
Er zijn 7x6x4=168 mogelijkheden om determinant 1 te vinden. Er zijn $2^9=512$ mogelijke matrices te vormen met nullen en enen.
De kans dat een 3×3 matrix met natuurlijke elementen oneven is , is dus
$\frac{168}{512}$

Geplaatst op 23 maart 2024 door admin

Gegeven een matrix $A=\begin{pmatrix}a&b\\c&d\end{pmatrix}$ .
Zijn determinant is
$det A =ad-bc$
Een product van twee natuurlijke getallen is oneven als beide getallen oneven zijn, dus de kans dat $ad$ oneven is, is $\frac{1}{4}$ . De kans dat $ad$ even is, wordt dat $\frac{3}{4}$ .
Nu is $det A$ even als $ad$ en $bc$ beiden even zijn of beide oneven zijn.
De kans dat $det A$ even is , is bijgevolg gelijk aan $\frac{1}{4}.\frac{1}{4}+\frac{3}{4}.\frac{3}{4}=\frac{10}{16}=0,625$