Een Pythagorees drietal is een drietal positieve gehele getallen (a,b,c) waarvoor geldt dat  . Zo is (3,4,5) een Pythagorees drietal omdat
. Zo is (3,4,5) een Pythagorees drietal omdat 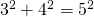 . De naam komt van de stelling van Pythagoras, aangezien dergelijke getallen kunnen optreden als de zijden van een rechthoekige driehoek met c als lengte van de schuine zijde.
. De naam komt van de stelling van Pythagoras, aangezien dergelijke getallen kunnen optreden als de zijden van een rechthoekige driehoek met c als lengte van de schuine zijde.
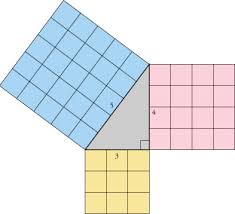
Een Pythagorees (a,b,c) drietal heet primitief als de grootste gemene deler van a,b en c gelijk is aan 1. Zo is (3,4,5) primitief , maar ( 6,8,10) niet.
Wat hebben complexe getallen hiermee nu te maken? Neem een complex getal z = a+ bi met a en b geheel. We spreken dan van een complex geheel getal. Definieer de norm N(z) van het complex getal als 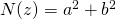 . Het is duidelijk dat de norm multiplicatief is, m.a.w.
. Het is duidelijk dat de norm multiplicatief is, m.a.w.  . Maar dan is
. Maar dan is
![Rendered by QuickLaTeX.com \[N(z^2)=(N(z))^2\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-368bc15c30b1b64b057a6135590bfee1_l3.png?media=1678572382)
De betrekking  kan je dus herschrijven als
kan je dus herschrijven als 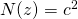 met
met 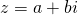 . We zijn dus op zoek naar complexe gehele getallen waarvan de norm een volkomen kwadraat is. Maar bovenstaande formule leert ons dat de norm van een complex getal een volkomen kwadraat is als het zelf een volkomen kwadraat is. Om een Pythagorees drietal te construeren, nemen we dus een willekeurig complex geheel getal en kwadrateren we dit getal. Dit kwadraat zal een complex getal zijn
. We zijn dus op zoek naar complexe gehele getallen waarvan de norm een volkomen kwadraat is. Maar bovenstaande formule leert ons dat de norm van een complex getal een volkomen kwadraat is als het zelf een volkomen kwadraat is. Om een Pythagorees drietal te construeren, nemen we dus een willekeurig complex geheel getal en kwadrateren we dit getal. Dit kwadraat zal een complex getal zijn 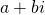 zijn, waarvan de norm
zijn, waarvan de norm  een volkomen kwadraat is.
een volkomen kwadraat is.
Neem bijvoorbeeld het complex getal  . Dan is
. Dan is 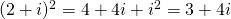 . De norm van dit kwadraat is
. De norm van dit kwadraat is  . Hiermee correspondeert het Pythagorees drietal
. Hiermee correspondeert het Pythagorees drietal  .
.
Vertrekken we algemeen van het complex geheel getal  . Kwadrateren we
. Kwadrateren we  :
: 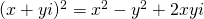 . De norm hiervan is
. De norm hiervan is  Zo krijgen we de gekende formule voor een willekeurig Pythagorees drietal
Zo krijgen we de gekende formule voor een willekeurig Pythagorees drietal
![Rendered by QuickLaTeX.com \[(x^2-y^2,2xy,x^2+y^2)\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-1e19d6cf128ea7a4dfd6cbe8608eebc3_l3.png?media=1678572382)
Als x en y onderling ondeelbaar zijn , dan is het zo gevormde Pythagorees drietal primitief. Bijgevolg hebben we aangetoond dat met deze constructie via kwadraten van complexe gehele getallen 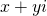 met x en y onderling ondeelbaar, elk primitief Pythagorees drietal kan worden verkregen.
met x en y onderling ondeelbaar, elk primitief Pythagorees drietal kan worden verkregen.