Grieks wiskunde : deel 8

Geplaatst op 27 oktober 2021 door admin

Apollonius van Perga (262-180 v.C.) is na Euclides en Archimedes, de derde en laatste grote Griekse wiskundige.

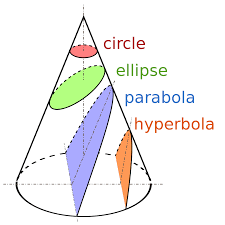
Hij is de auteur van de beroemde verhandeling in 8 delen : de Konica, over kegelsneden. Hierin definieert hij de kegelsneden als vlakke doorsneden van kwadratische kegels en ontwikkelt hij, in een klare en zuiver meetkundige stijl, een studie van deze krommen.

Gebruik makend van methodes van de meetkundige algebra, stelt hij de kegelsneden voor door hun zogenaamde symptoom . Voor ons betekent dit niet minder of meer een carthesische vergelijking. Het hoeft ons dan ook niet te verwonderen dat dit werk van Apollonius aan de basis ligt van latere studies van Descartes en Fermat, waaruit de moderne analytische meetkunde is ontstaan.

Vierkantswortel benaderen

Geplaatst op 22 oktober 2021 door admin

Een eenvoudige manier om vierkantswortels te benaderen zonder rekentoestel. Noteer met y het kwadraat het dichts bij x. Dan is

$\sqrt{x}\approx \frac{x+y}{2\sqrt{y}}$

Voorbeeld 1: $\sqrt{23}\approx \frac{23+25}{2*5}=4,8$ . Met rekentoestel vind je als waarde 4,795831523…

Voorbeeld 2; $\sqrt{50}\approx \frac{50+49}{2*7}\approx7,0714$ . Met rekentoestel vind je als waarde 7,071067812…

9801

Geplaatst op 17 oktober 2021 door admin

Mooie decimale schrijfwijze! Kan je dit verklaren?

Nu is $\frac{1}{99}=0,01010101...=\sum_{n=1}^{\infty}\frac{1}{100}$ . Verder is $\frac{1}{9801}=\Big(\frac{1}{99}\Big)^2$ .

Je kan gemakkelijk narekenen dat

$\Big(\sum_{n=1}^{\infty}x^n\Big)^2=x.\sum_{n=1}^{\infty}nx^n$

Vervangen we nu hierin x door $\frac{1}{99}$ , dan krijgen we de gewenste decimale schrijfwijze. Maar waarom ontbreekt hierin de 98?

In de uitwerking staan de som $\frac{98}{100^{98}}+\frac{99}{100^{99}}\frac{100}{100^{100}}=\frac{1}{100^{100}}(980000+9900+100)=\frac{99}{100^{98}}$ .