Tag archieven: oppervlakte cirkel

Sangaku 2

Geplaatst op door

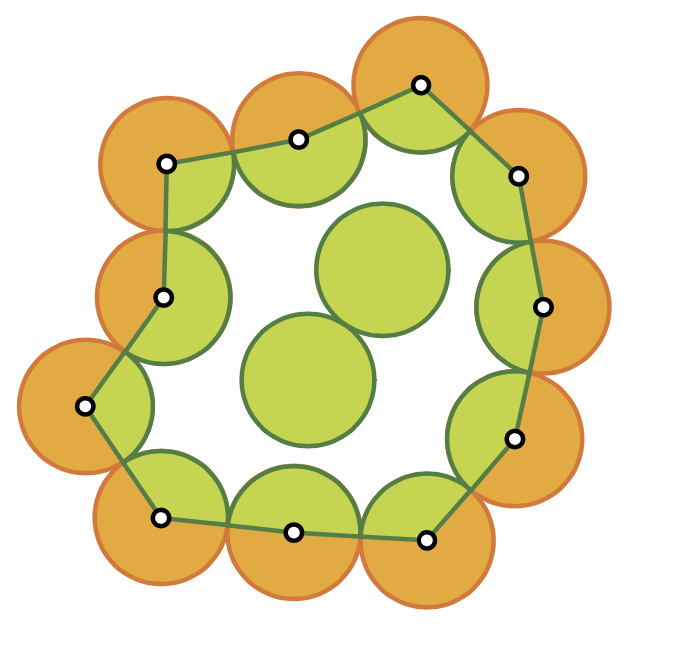
Dit probleem komt uit de verzameling Siri Shinpen van Saito Gigi (1816-1889). Het werd door Nakasone Munekuni voorgesteld in 1856 en opgehangen in de Haruna schrijn in Haruna.

Antwoord

  • Te bewijzen is dat de groene oppervlakte en de oranje oppervlakte gelijk zijn.
  • De groene oppervlakte  bestaat uit 2 cirkels (2\pi r^2) en n cirkelsectoren. De oppervlakte van een cirkelsector is \frac{1}{2}r^2\alpha.
  • Als we al de oppervlaktes van die sectoren optellen vinden we 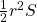\frac{1}{2}r^2S met S de som van al de hoeken van de getekende veelhoek. Dus is S=(n-2)\pi. 
  • De groene oppervlakte is dus \frac{n+2}{2}\pi r^2.
  • De oranje oppervlakte bekomen we door n cirkels te verminderen met een deel van de groene oppervlakte: \pi nr^2-\frac{n-2}{2}\pi r^2 en na vereenvoudiging is dat ook \frac{n+2}{2}\pi r^2.