Om het begrip afstand te definiëren hebben we een metriek nodig. Dit kan je hier lezen. Een voorbeeld van een metriek in ![]() is de Euclidische afstand, gedefinieerd door
is de Euclidische afstand, gedefinieerd door
![]()
Hiermee is een norm gedefinieerd via
![]()
en dan is
![]()
In ![]() is er ook een skalair product
is er ook een skalair product
![]()
Dit is een product met volgende eigenschappen:
 en
en 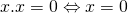 .
.

Het gegeven skalair product definieert dus de Euclidische metriek, via ![]() . Maar dat is niet altijd zo. Er zijn metrieken waarmee geen skalair product is geassocieerd. Een voorbeeld is de Manhattan metriek
. Maar dat is niet altijd zo. Er zijn metrieken waarmee geen skalair product is geassocieerd. Een voorbeeld is de Manhattan metriek
![]()
Er is geen skalair product dat hiermee correspondeert.
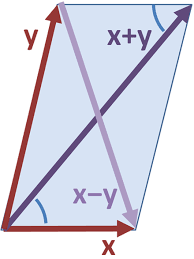
Normen die voldoen aan de parallellogram eigenschap kunnen een skalair product definiëren, andere niet:
![]()