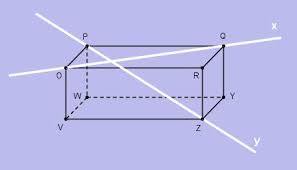
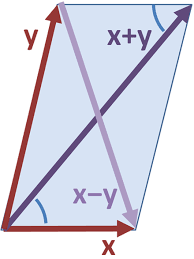
In het zesde jaar van het MO wordt een cursus gegeven over ruimtemeetkunde. In dit artikel wordt een andere manier van benadering gegeven dan de meeste handboeken. We steunen op de theorie van de vectorruimten. We onderscheiden twee delen:
- Definitie van punten, vectoren, rechten en vlakken. We bespreken hun onderlinge ligging en evenwijdigheid en bewijzen een aantal stellingen daarrond. Dit vindt je hier.
- Via de definitie van een skalair product kunnen we ook spreken over loodrechte stand, afstanden en hoeken. De bespreking daarvan vindt je hier.