Een rij ![]() voldoet aan een lineaire recurrentie als
voldoet aan een lineaire recurrentie als
![]()
De rij ![]() noemt men dan een lineaire recursieve rij.
noemt men dan een lineaire recursieve rij.
De karakteristieke veelterm van bovenstaande lineaire recurrentie is de veelterm
![]()
Als we ![]() in
in ![]() kunnen ontbinden als
kunnen ontbinden als
![]()
dan voldoet ![]() aan de lineaire recurrentie als en slechts als er functies
aan de lineaire recurrentie als en slechts als er functies ![]() , met graad kleiner of gelijk aan
, met graad kleiner of gelijk aan ![]() , bestaan zodat
, bestaan zodat
![]()
Als ![]() , dan zijn alle functies
, dan zijn alle functies ![]() constanten.
constanten.
Enkele speciale gevallen:
- Bij een rekenkundige rij is
 met
met  . Dit is geen lineaire recurrentie. Maar nu is ook
. Dit is geen lineaire recurrentie. Maar nu is ook  . Aftrekken van de twee formules geeft :
. Aftrekken van de twee formules geeft : 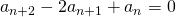 . Dits is wel een lineaire recurrentie met karakteristieke veelterm
. Dits is wel een lineaire recurrentie met karakteristieke veelterm  . Bijgevolg is
. Bijgevolg is 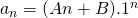 . Het is duidelijk dat
. Het is duidelijk dat  , de beginterm van de rij en
, de beginterm van de rij en 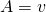 , het verschil van de rij. Zodoende is het algemeen voorschrift
, het verschil van de rij. Zodoende is het algemeen voorschrift 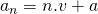 voor
voor 
- Bij een meetkundige rij is
 met
met  . Dit is een lineaire recurrentie met karakteristieke veelterm
. Dit is een lineaire recurrentie met karakteristieke veelterm  . Bijgevolg is
. Bijgevolg is 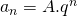 . Uit
. Uit  volgt dat
volgt dat 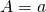 en dus is het algemeen voorschrift
en dus is het algemeen voorschrift  voor
voor 
Voorbeeld : ![]() en
en ![]() en elke ander term is het rekenkundig gemiddelde van de twee vorige termen. Een aantal termen van de rij:
en elke ander term is het rekenkundig gemiddelde van de twee vorige termen. Een aantal termen van de rij: ![]() . Om de algemene term van de rij te bepalen, zoeken we eerst de karakteristieke veelterm van de lineaire recurrentie:
. Om de algemene term van de rij te bepalen, zoeken we eerst de karakteristieke veelterm van de lineaire recurrentie: ![]() . Dan is
. Dan is ![]() . Bijgevolg is
. Bijgevolg is ![]() . Om A en B te bepalen gebruiken we dat
. Om A en B te bepalen gebruiken we dat ![]() en
en ![]() . Hieruit volgt dat
. Hieruit volgt dat ![]() en
en ![]() , zodat
, zodat ![]()
