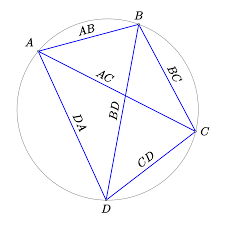
De kans, dat 4 willekeurig gekozen punten in het vlak, op 1 lijn of 1 cirkel liggen is erg klein. Er moeten dus wel speciale voorwaarden zijn om dit te doen gebeuren. Zo een voorwaarde wordt gegeven in de stelling van Ptolemaeus:
Voor 4 willekeurige punten A,B,C en D in het vlak, geldt ![]()
Enkele gevolgen:
- Als ABCD een koordenvierhoek is en ABC een gelijkzijdige driehoek, dan is
 .
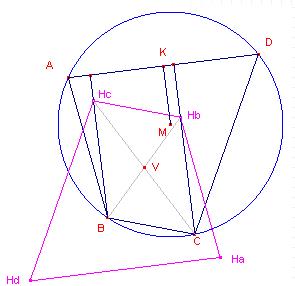
. - Als ABCD een koordenvierhoek is en de hoeken in B en D zijn recht, dan is
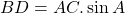 ( schrijf de hoek A als som van twee hoeken en pas de domformule voor
( schrijf de hoek A als som van twee hoeken en pas de domformule voor 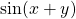 toe)
toe)