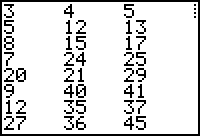Categorie archieven: Discrete wiskunde

Vierkanten en rechthoeken op een schaakbord

Geplaatst op door

Hoeveel vierkanten en rechthoeken kan men vormen op een n x n schaakbord?

  • Nemen we eerst het aantal vierkanten. We noteren V(n) voor het aantal vierkanten dat je kan tekenen op een nxn bord. Voor de 1×1 vierkanten heb je n mogelijke verticale posities en n horizontale, dus n^2 mogelijke vierkanten. Voor de 2×2 vierkanten heb je n – 1 verticale en horizontale mogelijke plaatsingen , dus (n-1)^2 mogelijkheden. Uiteindelijk is het totaal aantal vierkanten gelijk aan n^2+(n-1)^2+\cdots+2^2+1^2. 

        \[V(n)=\frac{n(n+1)(2n+1)}{6}\]

  • Met R(n) noteren we het aantal rechthoeken dat je kant tekenen op een nxn schaakbord. Voor een rechthoek heb je 2 verticale en twee horizontale lijnen nodig. Er zijn n+1 verticale en n+1 horizontale lijnen op een schaakbord. Om de verticale lijnen te kiezen heb je dus {n+1}\choose{2} =\frac{n(n+1)}{2}  mogelijkheden. Idem voor de keuze van de twee horizontale lijnen. Dus

        \[R(n)=\frac{n^2(n+1)^2}{4}\]

  • Voor een 8×8 schaakbord heb je dus 204 vierkanten en 1296 rechthoeken. Van die rechthoeken zijn er 1092 die geen vierkant zijn.

Delannoy getallen

Geplaatst op door

Beschouw in het vlak de punten P(x,y) met  natuurlijke getallen als coördinaten .Je kan je verplaatsen in het vlak volgens de vectoren (1,0) , (0,1)  en (1,1). Het aantal manieren waarop men vanuit de oorsprong het punt P(m,n) kan bereiken noemt men het Delannoy getal d(m,n), vernoemd naar de Franse legerofficier en amateur wiskundige Henri-Auguste Delannoy (28 sept 1833 – 5 febr 1915). Bij definitie stellen we d(0,0)=1.

Onderstaande tekening laat zien dat er bijvoorbeeld 13 mogelijke manieren zijn om het punt P(2,2) te bereiken:

Een tabel met enkele waarden van de Delannoy getallen :

We geven enkele eigenschappen:

  • d(m,0) = d(0,n) = 1
  • Er is een recursief verband tussen deze getallen: d(m,n) = d(m – 1,n) + d(m,n – 1) + d(m – 1,n – 1): elk getal in bovenstaande tabel is de som van zijn linkerbuur, zijn bovenbuur en het getal linksboven. Dit wordt beter geïllustreerd als we de tabel geven in de vorm van de driehoek van Pascal. ( teken de diagonalen van bovenstaande tabel). Nu is elk getal de som van de driehoek erboven.
  • We stellen de verplaatsingen over (1,0), (0,1) en (1,1) respectievelijk voor door O,N en D. Wanneer we k keer D gebruiken om P(m,n) te bereiken,  moeten we m – k keer O en n – k keer N gebruiken. Om te berekenen op hoeveel manieren dit kan, maken we gebruik van de formule van de herhalingspermutaties : we moeten
    k + (m – k) + (n – k ) = m + n – k symbolen rangschikken, waarvan er k van het soort D zijn , m – k van het soort O en  n – k van het soort N. We vinden dus voor elke waarde van k kleiner of gelijk aan het minimum van m en n als aantal mogelijkheden:

        \[\dfrac{(m+n-k)!}{k! (m-k)! (n-k)!}\]

    In het totaal heb je dan :

        \[\sum_{k=0}^{ min(m,n)}\dfrac{(m+n-k)!}{k! (m-k)! (n-k)!}\]

  • Op de tweede rij en tweede kolom vinden we alle oneven getallen :
    d(m,1) = 2m+1. Dit is gemakkelijk te bewijzen met bovenstaande formule

Een combinatorisch probleem

Geplaatst op door

Je beschikt over 7 verschillende flessen wijn en je hebt 7 proevers.  Het is niet praktisch alle 7 proevers alle 7 flessen te laten beoordelen, dus besluiten we volgende test te doen:

  • Iedereen proeft van  eenzelfde aantal flessen.
  • Elk paar van flessen wordt door exact 1 gemeenschappelijke persoon geproefd.
  • Elk paar van proevers proeft exact 1 gemeenschappelijke wijn.

Kan die test worden uitgevoerd? En wat als je de 7 vervangt door een ander aantal? Dit type van problemen is van groot belang voor statistici en behoort tot de tak van de combinatorische ontwerp theorie. Voor 7 is het probleem oplosbaar. Geef de 7 proevers een nummer van 1 tot 7 en de flessen een label A tot G. De test kan dan worden uitgevoerd door iedereen 3 flessen te laten proeven:
1:{A,B,C}   2:{A,D,F}   3: {B,D,E}   4:{A,E,G}   5: {C,E,F}    6:{B,F,G}   7:{C,D,G}

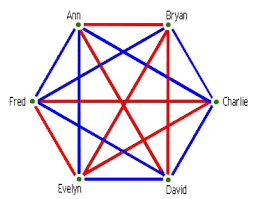
Deze oplossing heeft ook een mooie grafische voorstelling in volgende figuur waar de proevers voorgesteld worden door lijnen en de flessen door punten. Je moet dus 7 lijnen tekenen tussen 7 punten zodat elk paar punten juist 1 lijn gemeen heeft en zodat elk paar lijnen juist 1 punt gemeen heeft.

 

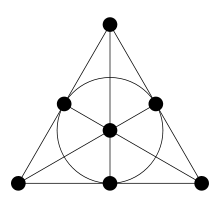
Je kan in ons voorbeeld 7 veranderen door een getal n van de vorm : n=q^2+q+1 met q een priemmacht. De overeenkomstige voorstelling geeft dan een projectief vlak van orde q+1. Dit vlak heeft q^2+q+1 punten en q^2+q+1 lijnen . Elke lijn bevat juist q+1 punten en door elk punt gaan exact q+1 lijnen. In bovenstaand voorbeeld is q=2.

Pythagorese drietallen

Geplaatst op door

Een Pythagorees drietal is een drietal positieve gehele getallen (a,b,c) waarvoor geldt dat

    \[a^2+b^2=c^2\]

Deze afbeelding heeft een leeg alt-attribuut; de bestandsnaam is pyt1.png

Zo zijn (3,4,5) en (5,12,13) allebei Pytagorese drietallen.
Het is duidelijk dat als (a,b,c) een Pythagorees drietal is, dat dan ook (ad,bd,cd) een Pythagorees drietal is. Oplossingen van a^2+b^2=c^2 die relatief ondeelbaar zijn, noemen we primitieve Pythagorese drietallen. Hiervoor kennen we volgend resultaat:


Als m en n relatief ondeelbare postieve gehele getallen zijn met m>n en waarbij één ervan even is en de andere oneven, dan vormen  a=m^2-n^2, b=2mn en c=m^2+n^2 een primieteve oplossing van a^2+b^2=c^2. Bovendien geldt dat elke primitief Pythagorees drietal van die vorm moet zijn, op een mogelijke permutatie van a en b na.

Spelen met kralen

Geplaatst op door

Hoeveel snoeren kan je maken met 3 rode en 5 witte kralen? Als je het snoer draait (cyclisch) of omkeert ( spiegeling), krijg je geen ander snoer.

We stellen een snoer voor als een combinatie van 3 R-en en 5 W’s. We weten dat WRRRWWWW en RRRWWWWW dezelfde ketting voorstelt. We kunnen er dus steeds voor zorgen dat we eindigen met een R. Maar ook RRWRWWWW en RWRRWWWW stellen hetzelfde snoer voor, want als je de laatste 4 W’s vooraan zet, zijn de twee snoeren elkaars spiegelbeeld.

Focussen we ons even op de rode kralen en bekijken we een snoer als
…R…R…R, dan rest ons de 5 witte kralen te verdelen over de drie aangegeven vakjes (na de laatste R is er geen vakje meer wegens het cyclisch zijn van het snoer. We coderen het snoer door de aantallen witte kralen in die vakjes. De combinatie WRRRWWWW en RRRWWWWW of WWWWWRRR stellen we dan voor als 500 en de gelijke snoeren RRWRWWWW en RWRRWWWW worden dan 401 en 410. We kiezen voor  die getallencombinatie die een niet -stijgende rij is.

Welke mogelijkheden houden we uiteindelijk over?

RRRWWWWW=500
RRWRWWWW=401=410
RRWWRWWW=302=320
WRWRWWWR=113=311
WRWWRWWR=122=221

En dus is het aantal snoeren gelijk aan het aantal partities van 5 in hoogstens 3 delen, dit is het aantal manieren om 5 te schrijven als de som van hoogstens 3 postieve getallen. Kunnen we dit veralgemenen?  3 rode en n witte kralen? Lees hierover meer in volgens artikel.