Tag archieven: priemgetallen

Priemgetallen

Geplaatst op door

De Poolse wiskundige W.Sierpinski (1882-1969) was eer gefascineerd door de priemgetallen en hun spreiding tussen de andere natuurlijke getallen. We vermelden twee mooie resultaten.

Men kan een rij van opeenvolgende natuurlijke getallen bepalen, zo lang als men wilt, die geen enkel priemgetal bevat. Zo kan men bijvoorbeeld 100 opeenvolgende getallen kiezen zonder dat er een priemgetal inzit.  Neem 101!+2,101!+3,…,101!+101. Dit zijn 100 opeenvolgende getallen en ze zijn geen van allen priem want ze zijn respectievelijk deelbaar door 2,3,…,101

Voor elke n kan men een priemgetal vinden met links en rechts ervan n niet-priemen:

  • Neem een priemgetal q groter dan n+1.
  • Bereken a=\prod_{j=1}^{q-2}(q^2-j^2).
  • q  is onderling ondeelbaar met a.
  • De stelling van Lejeune-Dirichlet over de rekenkundige rij zegt dat er een priemgetal p bestaat met p>q en p=ak+q.
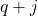  • Nu is q+j een deler van a en omdat p+j=ak+q+j ook een deler van p+j. 
  • Analoog is q-j een deler van p-j.
  • Dus zijn p-j en p+j niet priem en dit voor j=1,2,…,n

Neem n=2 en q respectievelijk de priemgetallen 5,7,11,13,…, dan kan je zo bewijzen dat er oneindig veel priemgetallen bestaan die geen deel uitmaken van een priemtweeling.

Spiraal van Ulam

Geplaatst op door

Je kan volgend rooster van natuurlijke getallen maken in de vorm van een spiraal:

De wiskundige Stanislaw Ulam kreeg in 1963 het idee om e priemgetallen hierbij aan te duiden 

Hij zag, tot zijn verbazing, dat de priemgetallen de neiging hebben om zich op diagonalen van de spiraal te bevinden. De diagonalen zijn ook zichtbaar wanneer er heel veel getallen in een spiraal worden geplaatst. Het opvallende is, dat priemgetallen zich meer op bepaalde diagonalen bevinden dan op andere. De reden hiervoor is alsnog onduidelijk.

Priemtweelingen

Geplaatst op door

Een paar opeenvolgende priemgetallen waarvan de afstand 2 is, noemen we een priemtweelingen. Buiten de eerste priemtweelingen 3-5 vinden we bijvoorbeeld ook 5-7, 11-13, 17-19,… Ze ontstaan allemaal (behalve 3-5), door vertrekkend van 5-7, een translatie uit te voeren over 6 eenheden. Dit is logisch want een priemgetal is altijd van de vorm 6k+1 of 6k-1. 

Een Python programma om alle priemtweelingen kleiner dan 1000 te bepalen:
De output:

Een paar ‘leuke ‘ eigenschappen, die zeer eenvoudig te bewijzen zijn:

  • Een priemtweelingen heeft een symmetriemidden dat steeds een 6-voud is.
  • De som van twee elementen van een priemtweelingen is steeds een 12-voud.
  • De afstand voor de overeenkomstige elementen van twee priemtweelingen is steeds een 6-voud.
  • De afstand van het grootste getal van de kleinste priemtweeling tot het kleinste getal van de grootste priemtweelingen is een 6-voud min 1.
  • Er bestaat geen grootste priemtweeling.