Tag archieven: rakende cirkels
Sangaku 9
De stelling van Casey
Volgende stelling komt van de hand van de Ierse wiskundige Casey (1820-1891)
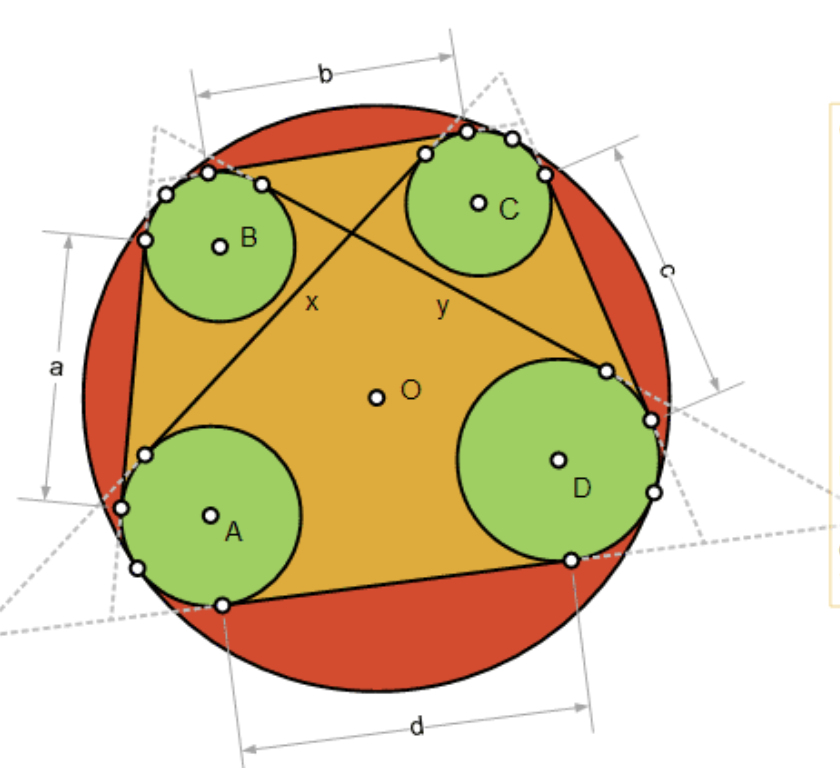
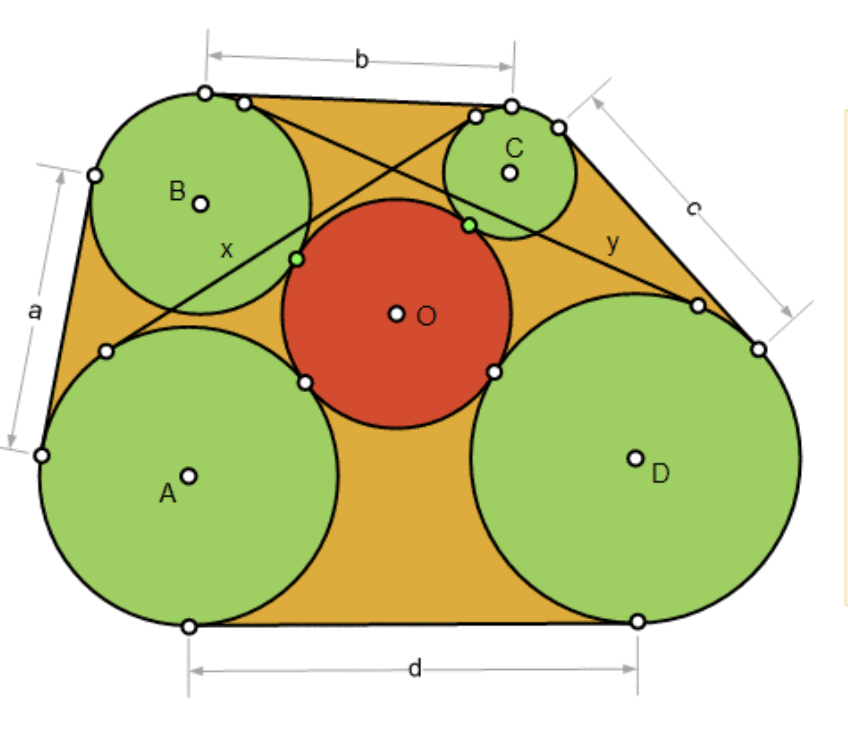
Gegeven is een cirkel, met middelpunt O en 4 niet snijdende cirkels, met middelpunten A,B,C en D) binnen die cirkel die in volgorde raken aan de grote cirkel. Noteer met aub,c,d,x en y hun gemeenschappelijke uitwendige raaklijnen. dan geldt:
![]()
Als we de 4 binnenste cirkels laten ‘ontaarden’ in 4 punten, krijgen we de stelling van Ptolemaeus. Andere varianten bestaan er in slechts enkele cirkels te laten krimpen tot punten. Het omgekeerde resultaat is eveneens geldig.
De stelling klopt trouwens ook als de 4 kleine cirkels aan de buitenkant liggen van de gegeven cirkel.
Dit artikel is het 500ste op deze website. Bedankt aan alle lezers.
Nootje 25
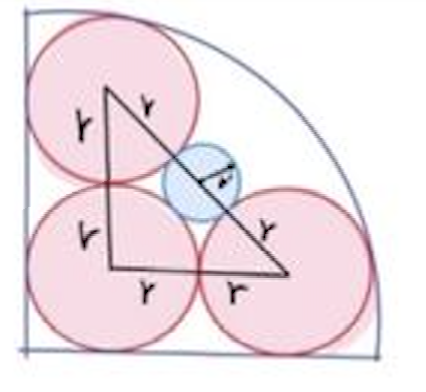
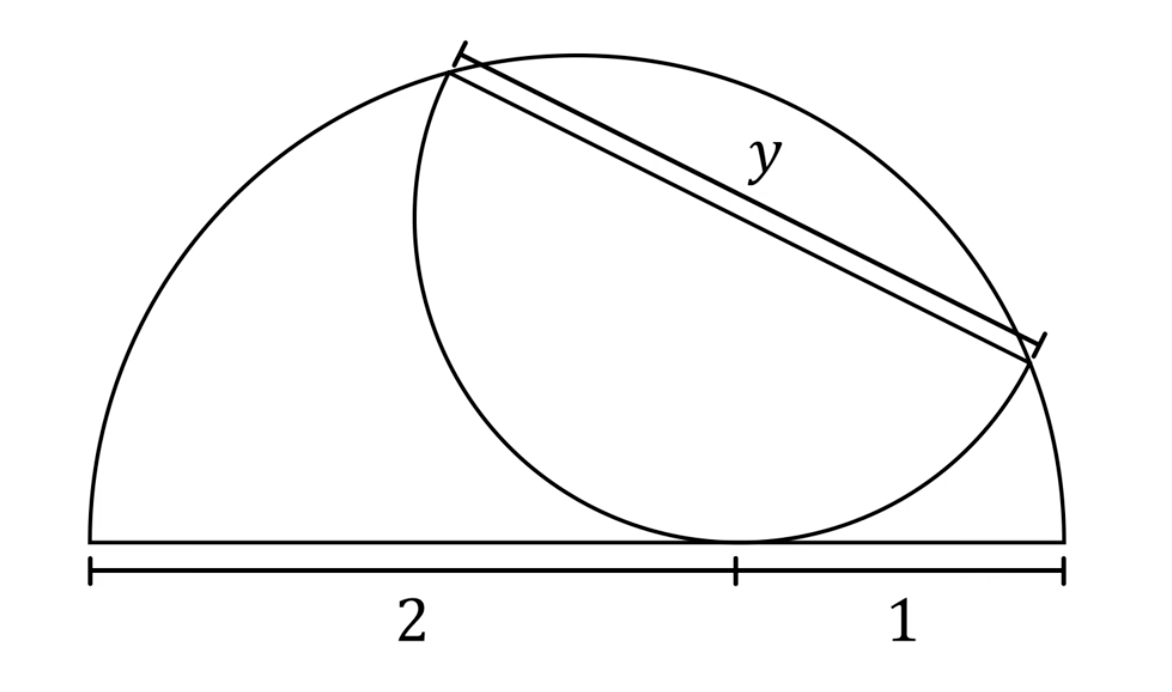
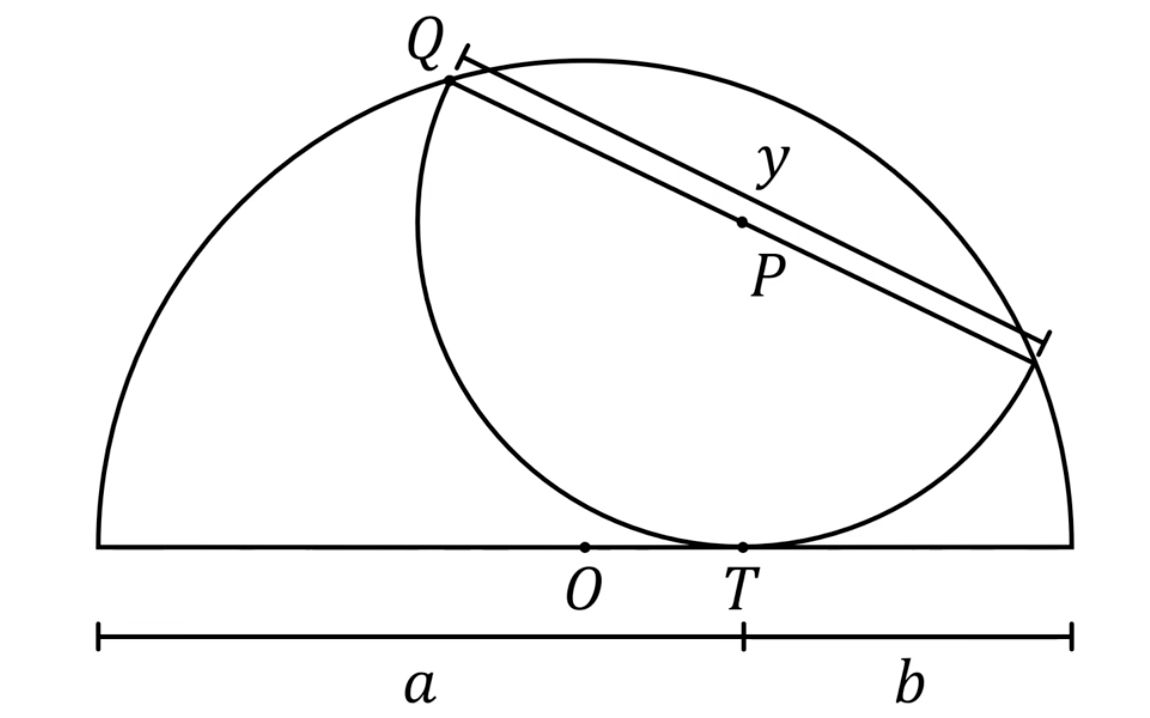
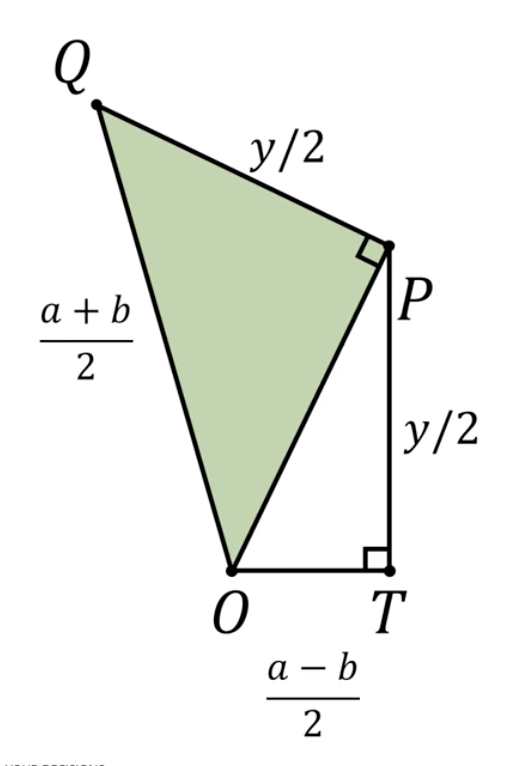
Bereken de lengte van de middellijn y.