Tag archieven: kleine nootjes

Nootje 55

Geplaatst op door

Bepaal de oppervlakte  van het blauwe deel, beschreven door twee halve cirkels in een vierkant met zijde 8 cm.

Antwoord

Bij dit soort opgaven is het handig om tekening te “herschikken”:

En dan is het duidelijk dat het blauwe gebied eigenlijk een half vierkant vormt. De oppervlakte is dan \frac{1}{2}8^2=32 vierkante centimeter.

Nootje 54

Geplaatst op door

Bereken de oppervlakte van volgende vierhoek:

Antwoord

  • We vervolledigen deze vierhoek tot een driehoek.

  • De tophoek is 30^\circ en via de definitie van sinus en tangens kan je de zijden berekenen in de bovenste kleine driehoek:  2 en \sqrt{3}.
  • In de grote driehoek kan je via de definitie van tangens de basis AD berekenen: \frac{4}{\sqrt{3}}.
  • De oppervlakte van de vierhoek ABCD is het verschil van de oppervlaktes van de grote en de kleine driehoek : \frac{8}{\sqrt{3}}-\frac{\sqrt{3}}{2}=\frac{13\sqrt{3}}{6}

 

 

Nootje 49

Geplaatst op door

De functie f is gedefinieerd op de verzameling geordende paren positieve getallen en voldoet aan :f(x,x)=x , f(x,y)=f(y,x) en f(x,y).(x+y)=y.f(x,x+y). Bereken f(14,52)

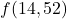
Antwoord

  • f(14,52)=f(14,14+38). Pas nu regel 3 toe:
  • f(12,52)=\frac{52}{38}f(14,38). Nu is 38=14+24. Pas opnieuw regel 3 toe en we krijgen:
  • f(12,52)=\frac{52}{24}f(14,14+10). Nogmaals regel 3:
  • f(12,52)=\frac{52}{10}f(14,10)
  • We draaien de argumenten om volgens regel 2 en we vinden 
  • f(12,52)=\frac{52}{10}f(10,14)
  • f(12,52)=\frac{52}{10}f(10,10+4)=\frac{52}{10}.\frac{14}{4}.f(10,4)
  • Omdraaien : f(12,52)=\frac{91}{5}.f(4,4+6)=\frac{91}{3}.f(4,4+2)
  • Nog maar een keer regel 3 geeft :f(12,52)=91.f(4,2)=91.f(2,2+2).
  • Uiteindelijk bekomen door regel 3 en regel 1 het antwoord:

        \[f(14,52)=91.2.f(2,2)=91.2.2=364\]