De intellectuele geschiedenis van Griekenland ontstaan is de Archaïsche periode ( 8 ste – 6 de eeuw voor Christus) in de stadstaten aan de boorden van de Egeïsche zee.
Deze steden zijn handelscentra die in contact komen met de Oosterse beschavingen. Zo wordt op het einde van de 7de eeuw v. C. , en ongetwijfeld uit Babylonische en Egyptische bronnen, de wiskunde, in het bijzonder de meetkunde, door Thales van Milete
( 624 v.C.-545 v.C.) geïntroduceerd.

Eerste van 7 wijzen, vader van de Griekse meetkunde, ziehier twee epitheta van Thales. De filosofen uit die tijd stelden zich tot doel orde te scheppen in de schijnbare wanorde van de ons omringende werkelijkheid. Ze probeerden een antwoord te vinden op de vraag naar het waarom der dingen. Geconfronteerd met de onbetrouwbare gegevens van de Babylonische en Egyptische wiskunde, probeerde Thales dan ook niet alleen de waarheid, maar ook het waarom van die resultaten te achterhalen en ze te ordenen. De Griekse meetkunde vertoont aldus van bij de geboorte haar karakter van deductieve wetenschap.
Volgende stellingen worden aan Thales toegeschreven:
- elke middellijn verdeelt de cirkel in twee congruente delen.
- de basishoeken van een gelijkbenige driehoek zijn gelijk.
- overstaande hoeken zijn gelijk.
- het congruentiekenmerk HZH.
Onder druk van de Perzische veroveringen in Klein-Azië verplaatst het centrum van de culturele activiteiten zich halfweg de 6de eeuw v.C. naar Zuid-Italië en Sicilië: hier komt men in de school van Pythagoras tot intensieve beoefening van de wiskunde.

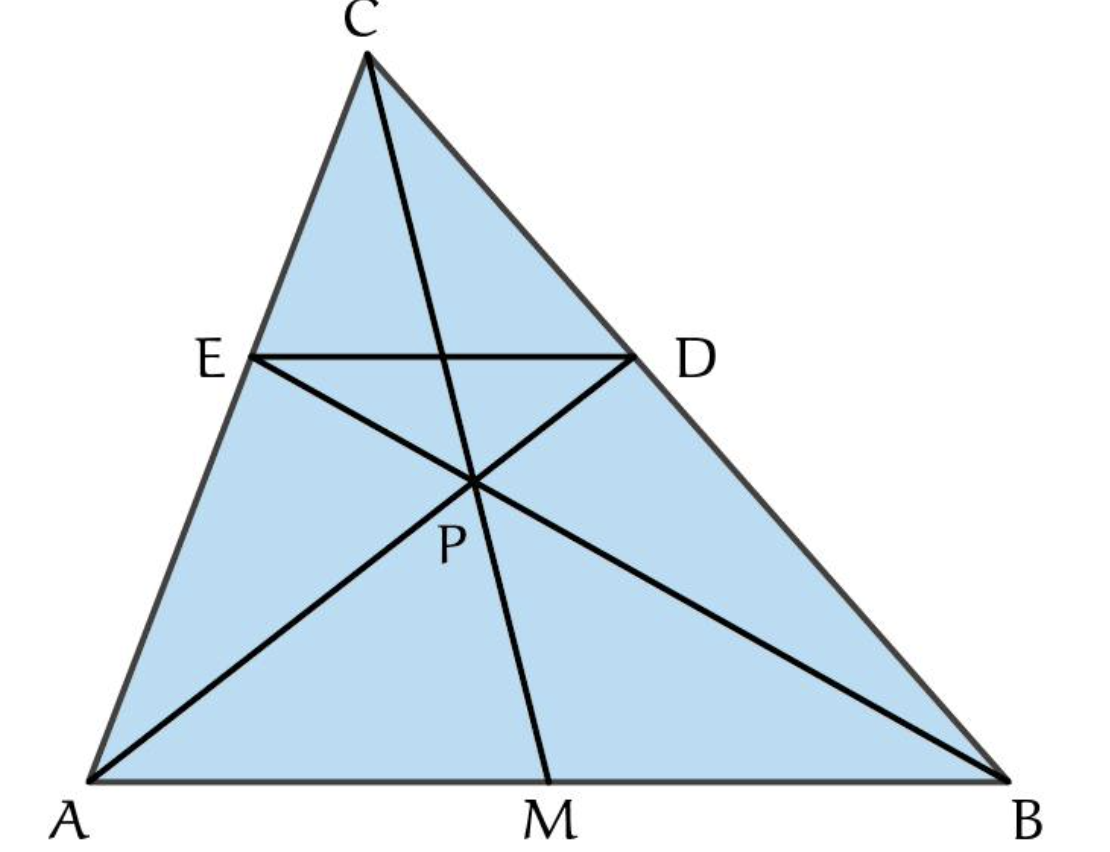
![Rendered by QuickLaTeX.com \[\frac{|AM|}{|MB|}.\frac{|BD|}{|DC|}.\frac{|CE|}{|EA|}=1\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-3b8fd1190ede464efd1fbfe021802489_l3.png?media=1678572382)
![Rendered by QuickLaTeX.com \[\frac{|BD|}{|DC|}.\frac{|CE|}{|EA|}=1\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-855e574b175406b5f55642e6d24465c1_l3.png?media=1678572382)