Maandelijks archief: december 2017

Vereenvoudig

Geplaatst op door

Als een probleem te moeilijk is om op te lossen, kan het oplossen van een ander, eenvoudiger probleem, dikwijls inspiratie geven om het oorspronkelijk probleem op te lossen. We kunnen bijvoorbeeld eerst speciale gevallen bestuderen of we kunnen bijvoorbeeld één van de voorwaarden weglaten. Of we kunnen concrete gevallen van het algemeen probleem proberen aan te pakken.

Gegeven is een willekeurige driehoek. Construeer een vierkant zodat alle hoekpunten van dat vierkant op de zijden van de driehoek liggen. Twee van de hoekpunten zijn dus gelegen op dezelfde zijde van de driehoek.

 


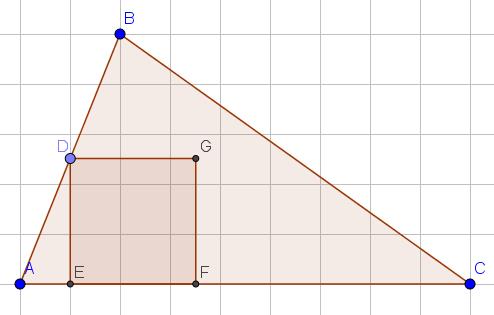
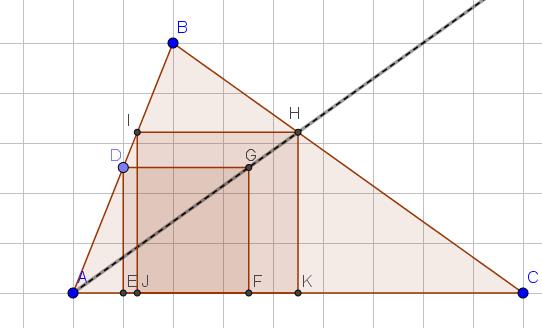
  • We laten één van de voorwaarden weg en proberen eerst een vierkant EDGF te construeren waarvan 2 punten op een zijde van de driehoek liggen en waarvan één ander hoekpunt op een andere zijde van de driehoek ligt.
  •  

    We gaan het vierkant vergroten zodat D op [AB] blijft en E en F ook op [A,C] blijven. Ondertussen zorgen we ervoor dat G op de derde zijde van de driehoek komt te liggen.We gebruiken hiervoor een homothetie met centrum A die G afbeeldt op H ( het snijpunt van AG met BC).

  •  

    Het homothetisch beeld van EDGF is dan JIHK en dit vierkant vodoet aan de gestelde voorwaarden.

    

    • 


					

		
		
	


				
					
	

		

						
Maak een tekening

			
						

				Geplaatst op   door  			

			
					


				

			
Soms kan het een grote hulp zijn de gegevens van het probleem te visualiseren. We denken dan uiteraard aan een meetkundig probleem waar een tekening ons kan helpen tot een oplossing te komen. Maar je kan ook werken met een Venndiagram, een boomschema of met grafen om je gedachten te ordenen.


Neem een driehoek ABC met hoeken \alpha,\beta en \gamma. Bewijs dan: 


      \[\dfrac{\sin \alpha+\sin \beta}{2}\leq \sin \dfrac{\alpha+\beta}{2}\]




    

  • Je kan proberen de ongelijkheid te bewijzen via een tekenschema. Nuttig hierbij zullen waarschijnlijk de formules van Simpson zijn.
    • 

  • Maar bekijken we eens de grafiek van de sinusfunctie. Veronderstel \alpha \leq \beta \leq \gamma. De hoeken zijn uiteraard allen kleiner dan 180^\circ.
    • 

  • A(\alpha,\sin \alpha) en B(\beta,\sin \beta). C is het midden van het lijnstuk [A,B].
    • 

  • Het linkerlid van de gegeven ongelijkheid is de hoogte van het punt C en het rechterlid de hoogte van het punt D. Door de bolle vorm van de grafiek van de sinusoïde in [0,\pi] is de ongelijkheid duidelijk.

    

    • 



 



					

		
		
	


				
					
	

		

						
Formules met binomiaalgetallen

			
						

				Geplaatst op   door  			

			
					


				

			
Het binomiaalgetal \binom{n}{p} berekent het aantal p-combinaties van n elementen; dit is het aantal mogelijkheden om p elementen te nemen uit n beschikbare elementen. Hierbij is  herhaling niet toegestaan en speelt de volgorde van de elementen geen rol.


Als 0 \leq p \leq n, dan kennen we de formule


      \[\binom{n}{p}=\dfrac{n!}{p!(n-p)!}\]




Om verbanden tussen de binomiaalgetallen te bewijzen kunnen we gebruik maken van bovenstaande formule. Vaak geeft dit aanleiding tot technisch moeilijk rekenwerk. Vandaar dat we in volgende sectie een andere werkmethode willen geven, steunend op eenvoudige begrippen uit de verzamelingenleer. Lees hierover volgend artikel.

					

		
		
	


				
					
	

		

						
Recursie

			
						

				Geplaatst op   door  			

			
					


				

			
Een rij van getallen kan je geven met behulp van een recursief  voorschrift zoals bijvoorbeeld : a_1=1 en a_n= 2a_{n-1}+1. Soms kan je uit dit recursief voorschrift een expliciete formule afleiden voor de algemene term van de rij. Soms kan dat niet, maar is het mogelijk, via recursie, de parameters te herleiden tot waarden waarvoor je het probleem wel kan oplossen.




Een eerlijk muntstuk wordt n keer opgeworpen. Wat is de kans op twee opeenvolgende keren kop ergens in de rij worpen?


    

  • Noteer met P_n de kans dat er nergens twee keer kop na elkaar voorkomt is de rij van n worpen.
    • 

  • Het is duidelijk dat P_1=1 en P_2=\frac{3}{4}.
    • 

  • Stel n>2. Dan zijn er twee mogelijkheden naargelang de eerste worp kop of munt is.
    • 

  • Als je eerst munt gooit, dan is de kans dat je nergens twee keer kop na elkaar hebt in de volgende n-1 worpen gelijk aan P_{n-1}.
    • 

  • Gooi je eerst kop, dan moet de tweede worp munt zijn, want anders zou je twee keer kop na elkaar hebben. De kans dat je nergens twee keer kop na elkaar hebt in de volgende n-2 worpen gelijk aan P_{n-2}.
    • 

  • Uit de vorige twee punten vinden we tenslotte dat

          \[P_n=\frac{1}{2}P_{n-1}+\frac{1}{4}P_{n-2}\]
    

    • 

  • Dit kan je herleiden tot 2^nP_n=2^{n-1}}P_{n-1}+2^{n-2}P_{n-2}. Of via S_n=2^nP_n:

          \[S_n=S_{n-1}+S_{n-2}\]
    

    • 

  • Dit is de rij van Fibonacci, waarbij S_n het n+2 de getal in de rij van Fibonacci is. Dus S_n=F_{n+2}. De gezochte kans op twee opeenvolgende keren kop ergens in de rij van n worpen, met n>2 is dan X=1-P_n=1-\frac{F_{n+2}}{2^n}.
    • 


					

		
		
	


				
					
	

		

						
Bewijs door inductie

			
						

				Geplaatst op   door  			

			
					


				

			
Vaak bestaat een probleem erin aan te tonen dat een bepaalde eigenschap geldt voor elk natuurlijk getal. Hiervoor gebruiken we het principe van de  volledige inductie 


    

  •  Basisstap: Men bewijst P(1)
    • 

  •  Inductiehypothese: Men bewijst voor elke k dat als P(k) geldt, dan ook P(k+1) geldt.
    • 



Er bestaat ook een andere vorm, die we de sterke inductie noemen:


    

  • Basisstap: Men bewijst P(1) .
    • 

  •  Inductiehypothese: Men bewijst voor elke k dat als P(1),P(2),\ldots,P(k) gelden, dan ook P(k+1) geldt.
    • 



Voor elk natuurlijk getal n geldt :




      \[1^2+2^2+\ldots+n^2=\frac{1}{6}n(n+1)(2n+1)\]




    

  • De geldigheid van de formule voor n=1 is duidelijk, want  1^2=\frac{1}{6}.1.(1+1)(2+1). Dit is de basisstap.
    • 

  • De inductiehypothese : stel dat de formule ook geldt voor n=k. Dan is: 

          \begin{align*}1^2+2^2+\ldots+k^2+(k+1)^2=&(1^2+2^2+\ldots+k^2)+(k+1)^2\\=& \frac{1}{6}k(k+1)(2k+1)+(k+1)^2\\=&\frac{1}{6}(k+1)(2k^2+7k+6)\\=&\frac{1}{6}(k+1)(k+2)(2k+3) \end{align*}
    

     en dit is precies de formule voor n=k+1
    •