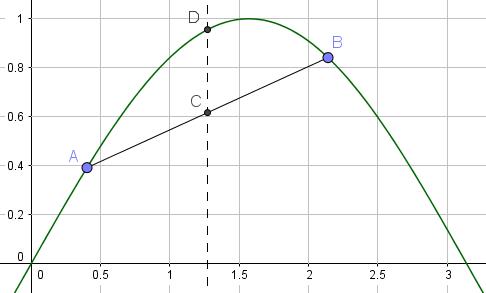
Het lijkt paradoxaal, maar soms kan een probleem vereenvoudigd en dus meer handelbaar en verstaanbaar gemaakt worden door het te veralgemenen. Een meer algemenere formulering opent soms bredere perspectieven, laat de niet essentiële zaken weg en voorziet ons soms van een nieuw arsenaal van technieken.
Wat is het grootst:
![]()
- De derde macht nemen van beide getallen lijkt erg ingewikkeld te worden.
- Probeer het meer algemeen probleem op te lossen: Wat is het grootst:
![Rendered by QuickLaTeX.com A=\sqrt[3]{4(x+y)}](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-a4c014dda31ae96d1254cff83df6b8ed_l3.png?media=1678572382) of
of ![Rendered by QuickLaTeX.com B=\sqrt[3]{x}+\sqrt[3]{y}](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-4b32563ba6e849f7bee2745ea858568d_l3.png?media=1678572382) ? Hierbij zijn
? Hierbij zijn  en
en  positief. De opgave is dan het speciaal geval met
positief. De opgave is dan het speciaal geval met  en
en 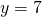 .
. - Stel
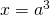 en
en 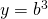 . Dan is
. Dan is  . Verder is
. Verder is 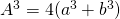 .
. - Nu is
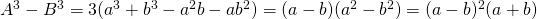 . Omdat
. Omdat  en
en  positief zijn, zijn ook
positief zijn, zijn ook  en
en  positief en is
positief en is 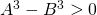 . Hieruit volgt dat
. Hieruit volgt dat  en dus ook dat
en dus ook dat  .
. - We besluiten dat
![Rendered by QuickLaTeX.com \sqrt[3]{60}](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-f4eac2d8b0a6ad36e7046bf9c3a39c11_l3.png?media=1678572382) groter is dan
groter is dan ![Rendered by QuickLaTeX.com 2+\sqrt[3]{7}](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-5189eb5d2f484afef09888502dfb7424_l3.png?media=1678572382) .
.