Pariteit

Geplaatst op 8 december 2017 door admin

Het feit dat een gegeven even of oneven is kan belangrijk zijn om de oplossing van het probleem te vinden. Het even of oneven zijn van een getal noemen we de pariteit van het getal. Deze heuristiek wordt dikwijls gebruikt in combinatie met kleuringen of het invariantie principe.

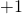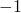Neem 2017 punten op een cirkel en verbind ze tot ze een 2017-hoek vormen. Elke zijde van deze 2017-hoek krijgt een ‘lading’: $+1$ of $-1$ . Bewijs dat er altijd een hoekpunt moet zijn, zodat het product van de ladingen van de zijden die samenkomen in dat punt, gelijk is aan $+1$ .

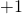Neem een willekeurige zijde en geef die lading 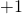$+1$ . Dit kan, want als alle ladingen 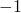$-1$ zouden zijn is het gestelde zeker al bewezen. Het rechtse eindpunt van de zijde noemen we $H_1$ .
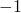Ga rechtsom en neem de volgende zijde. Is de lading +1 dan is $H_1$ een hoekpunt dat aan de voorwaarde voldoet. Dus veronderstel dat de lading $-1$ is.
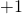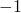Je gaat zo steeds verder. Ofwel vindt je twee maal na elkaar eenzelfde lading, en dan is de stelling bewezen. Ofwel alterneren de ladingen $+1$ en $-1$ elkaar. Omdat 2017 oneven is zal de laatste zijde lading +1 hebben en is de stelling ook dan bewezen.
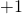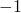Je kan het probleem ook oplossen door $P_i$ te definiëren als het product van de ladingen die in hoekpunt $H_i$ samenkomen. Het product van alle $P_i$ ’s moet $+1$ zijn, omdat alle zijden twee keer geteld worden in dit product. Omdat we een oneven aantal hoekpunten hebben kunnen niet alle $P_i$ ’s gelijk zijn aan $-1$ . 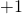Er is dus minstens één hoekpunt, zodat het product van de ladingen van de zijden die samenkomen in dat punt, gelijk is aan $+1$ .

De vergelijking van Pell

Geplaatst op 7 december 2017 door admin

Begin 17de eeuw. Door de Renaissance was de belangstelling voor de Griekse en Alexandrijnse cultuur weer opgewekt. Ook de werken van de oude wiskundigen werden herontdekt en heruitgegeven. Zo gaf Bachet (1557-1638) de werken van Diophantus in het Grieks en het Latijn uit. Pierre de Fermat (1601-1665) bestudeerde dat boek en loste vele problemen eruit op. In februari 1657 schreef Fermat een brief naar zijn landgenoot Frenicle (1602-1675) waarin hij vroeg om de diophantische vergelijkingen $x^2-61y^2=1$ en $x^2-109y^2=1$ op te lossen.

Frenicle deed meer: hij slaagde erin de vergelijking $x^2-Ay^2=1$ op te lossen voor alle niet-kwadratische waarden van $A \leq 150$ . Beide Fransen voerden een drukke correspondentie met de Engelse wiskundigen Wallis (1616-1703) en diens medewerker Lord Brouncker (1620-1684). Voor de sport aanvaardden ze de uitdaging om de vergelijkingen $x^2-151y^2=1$ en $x^2-313y^2=1$ proberen op te lossen. Wallis en Brouncker probeerden te bewijzen dat de vergelijking $x^2-Ay^2=1$ , voor niet-kwadratische waarden van A, altijd oplossingen heeft. Hieronder een afbeelding van John Wallis en Lord Brouncker

Pell (1611-1685) heeft een uitgave en vertaling van een boek waarin de oplossing hiervan staat, verzorgd, en Euler (1707-1783) heeft hem, per vergissing, ten onrechte de verdienste van de oplossing toegekend en tevens Pells nam verbonden aan die vergelijkingen, zoals blijkt uit een brief aan Lagrange (1736-1813). Lagrange was niet tevreden met het bewijs van de oplosbaarheid, zoals dat gegeven werd door Wallis. In 1768 slaagde hij erin een sluitend bewijs te vinden.

Het vinden van een oplossing is echter zeer lastig. Voor de diophantische vergelijking $x^2-Ay^2=-1$ is er zelfs niet altijd een oplossing.

Contradictie

Geplaatst op 5 december 2017 door admin

Redeneren door tegenspraak gaat uit van de veronderstelling dat de conclusie niet juist is en probeert door argumenteren te komen tot iets wat in tegenspraak is met gegeven is (de indirecte methode) of iets wat in tegenspraak is met iets waarvan we weten dat het waar is (reductio ad absurdum).

Bewijs dat de onderstaande reeks divergeert

$1+\frac{1}{2}+\frac{1}{3}+\cdots$

We veronderstellen dat de reeks niet divergeert maar dus convergeert naar de waarde $r$ .
Dus $r=(1+\frac{1}{2})+(\frac{1}{3}+ \frac{1}{4})+(\frac{1}{5}+ \frac{1}{6})+\cdots$ .
De eerste term van elk groepje van twee termen is groter dan de tweede, dus kunnen we schrijven dat
$r> (\frac{1}{2}+ \frac{1}{2})+ (\frac{1}{4}+ \frac{1}{4})+ (\frac{1}{6}+ \frac{1}{6})+\cdots = 1+\frac{1}{2}+ \frac{1}{3}+\cdots=r$

.
Dus is $r>r$ en dat is onmogelijk. Bijgevolg is de harmonische reeks niet convergent, maar wel divergent.

Het duivenhokprincipe

Geplaatst op 3 december 2017 door admin

Als je 5 ballen moet verdelen over 4 dozen, dan zal er een doos zijn met minstens 2 ballen. Immers de eerste 4 ballen kan je nog over de 4 dozen verdelen, maar voor het 5 de balletje is er geen doos meer over. Algemeen: verdeel je meer dan n objecten over n laden, dan bevat minstens één lade minstens 2 van die objecten. Dit eenvoudig principe werd voor het eerst expliciet gebruikt door Dirichlet (1805 – 1859) en wordt daarom ook het ladenprincipe of duivenhokprincipe van Dirichlet genoemd. Het principe kan in een nog algemenere vorm gegoten worden: Als je $kq+r$ ( met $q,r \in \mathbb{N}$ en $1<r<k$ ) objecten verdeelt over $k$ laden, dan is er minstens \’e\’en lade met minstens $q$ objecten.

Een voorbeeld:

Neem willekeurig $n+1$ getallen uit de verzameling $\{1,2,\cdots,2n \}$ . Bewijs dat er in die $n+1$ getallen steeds een getal bestaat dat deelbaar is door een ander van die $n+1$ getallen.

Neem $n+1$ getallen en noteer die door $a_1,a_2,\cdots,a_{n+1}$ en schrijf ze in de vorm $a_i=2^k.b_i$ waarin $b_i$ oneven is.
We hebben $n+1$ oneven getallen $b_i$ , allen uit het interval $\left[1,2n-1\right]$ .
In het interval $\left[1,2n-1\right]$ zijn er maar $n$ oneven getallen.
Volgens het duivenhokprincipe moeten er dus een $p$ en een $q$ bestaan zodat $b_p=b_q$ . Dan is één van de getallen $a_p$ of $a_q$ deelbaar door het andere.

Wiskunde is leuk

Maandelijks archief: december 2017

Pariteit

Neem 2017 punten op een cirkel en verbind ze tot ze een 2017-hoek vormen. Elke zijde van deze 2017-hoek krijgt een ‘lading’: $+1$ of $-1$ . Bewijs dat er altijd een hoekpunt moet zijn, zodat het product van de ladingen van de zijden die samenkomen in dat punt, gelijk is aan $+1$ .

De vergelijking van Pell

Contradictie

Bewijs dat de onderstaande reeks divergeert

$1+\frac{1}{2}+\frac{1}{3}+\cdots$

Het duivenhokprincipe

Neem willekeurig $n+1$ getallen uit de verzameling $\{1,2,\cdots,2n \}$ . Bewijs dat er in die $n+1$ getallen steeds een getal bestaat dat deelbaar is door een ander van die $n+1$ getallen.

Neem 2017 punten op een cirkel en verbind ze tot ze een 2017-hoek vormen. Elke zijde van deze 2017-hoek krijgt een ‘lading’: of . Bewijs dat er altijd een hoekpunt moet zijn, zodat het product van de ladingen van de zijden die samenkomen in dat punt, gelijk is aan .

Bewijs dat de onderstaande reeks divergeert

Neem willekeurig getallen uit de verzameling . Bewijs dat er in die getallen steeds een getal bestaat dat deelbaar is door een ander van die getallen.

Neem 2017 punten op een cirkel en verbind ze tot ze een 2017-hoek vormen. Elke zijde van deze 2017-hoek krijgt een ‘lading’: $+1$ of $-1$ . Bewijs dat er altijd een hoekpunt moet zijn, zodat het product van de ladingen van de zijden die samenkomen in dat punt, gelijk is aan $+1$ .

Bewijs dat de onderstaande reeks divergeert

$1+\frac{1}{2}+\frac{1}{3}+\cdots$

Neem willekeurig $n+1$ getallen uit de verzameling $\{1,2,\cdots,2n \}$ . Bewijs dat er in die $n+1$ getallen steeds een getal bestaat dat deelbaar is door een ander van die $n+1$ getallen.