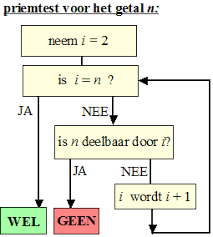
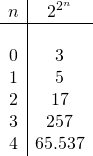Tag archieven: fermat

Geschiedenis van de kansrekening

Geplaatst op door

Waarschijnlijk zijn de eerste wiskundige discussies over kansen ontstaan bij gokkers uit de 17de eeuw die zich vragen stelden over spelletjes met dobbelstenen en speelkaarten. Deze gokkers vroegen raad aan de Franse wiskundige Blaise Pascal(1623-1662), die op zijn beurt hierover correspondeerde met Pierre de Fermat(1601-1665).

Ze gebruikten combinatorische methoden om sommige van deze vraagstukken op te lossen. In 1657 verscheen van de Nederlander Christiaan Huygens (1629-1695) het boek De Ratiociniis is Alea Ludo. Dit boek werd beschouwd als eerste invloedrijk werk over kansrekenen.

Stelling van Wilson

Geplaatst op door

De kleine stelling van Fermat zegt ons dat voor een priemgetal p geldt dat a^p \equiv a \mod{p}. Maar dan zijn 1,2, … , p – 1 allemaal nulpunten van de veelterm X^{p-1}-1 in de verzameling \mathbb{Z}_p[X] en dus kunnen we, omdat er geen nuldelers zijn, volgende ontbinding neerschrijven: X^{p-1}-1 = (X-1)(X-2) \cdots (X-(p-1)).
Door hierin X te vervangen door 0, vinden we een deel van volgende stelling:

    \[p \text{ is priem als en slechts als } (p-1)! \equiv -1 \mod{p}\]

Dit resultaat staat bekend als de stelling van Wilson, naar de Engelse wiskundige John Wilson (1741-1793). Nochtans komt dit resultaat een eerste keer voor bij Abu Ali al-Hasan ibn al-Haytham (965-1040)

Bovendien had Wilson geen bewijs van de stelling. Het was Lagrange die in 1771 het eerste bewijs ervan formuleerde.

Het is ook duidelijk dat als n een samengesteld getal is, groter dan 4,  dat  (n-1)! \equiv 0 \mod{n}.

Een algemene vorm is voor ieder oneven priemgetal p en voor ieder positief geheel getal k kleiner dan p:

    \[(k-1)!(p-k)! \equiv (-1)^k \mod{p}\]

Deze veralgemening danken we aan C.F.Gauss

Pseudopriemen

Geplaatst op door

De kleine stelling van Fermat leert ons dat voor een priemgetal p geldt dat

    \[a^{p-1} \equiv 1 \mod p\]

of voor getallen a die onderling ondeelbaar zijn met p: a^p \equiv a \mod p.

De stelling van Fermat is niet omkeerbaar. Inderdaad is  2^{340} \equiv 1 \mod 341 en 341 = 11 \times 31. In de vijfde eeuw voor onze jaartelling wisten de Chinezen al dat uit p priem volgt dat 2^{p-1} \equiv 1 \mod p. Zij waren ook overtuigd van het omgekeerde. Ook Leibniz was daarvan overtuigd. Slechts in 1819 vond F. Sarrus bovenvermeld tegenvoorbeeld.

We noemen 341 een pseudopriem t.o.v. de basis 2.

Een Carmichael getal is een getal  p dat niet priem is en waar voor alle a die onderling ondeelbaar zijn met p, toch geldt dat a^{p-1} \equiv 1 \mod p. Zo is bijvoorbeeld 561 het kleinste Carmichael getal. De volgende Carmichael getallen zijn  1105, 1729, 2465, 2821, 6601, 8911, 10585, 15841 en  29341. Pas in 1994 werd bewezen dat er oneindig veel Carmichael getallen zijn.

De naam Carmichael getal komt van de Amerikaanse wiskundige  Richard David  Carmichael ( 1979-1967) die het bestaan ervan introduceerde in 1910. Een andere naam voor deze getallen is absolute pseudopriemen

Priemgetaltest

Geplaatst op door

We willen twee fundamentele vragen uit de getaltheorie even onder de aandacht brengen:

  1. Hoe kan men snel zien of een getal een priemgetal is?
  2. Als n niet priem is, hoe vindt men gehele getallen a en b , groter dan 1, zodat n = a.b?

Het is verbazingwekkend dat men dikwijls kan weten dat een getal niet priem is, zonder er een factor van te kennen. Dat is te danken aan de stelling van Fermat: als n priem is dan geldt voor elk geheel getal a dat

    \[a^n \equiv a \mod n\]

Dus als je een geheel getal a kan vinden waarvoor a^n niet gelijk is aan a modulo n, dan weet men zeker dat n niet priem is, zonder nochtans een factor van n te kennen.

Willen we bewijzen dat een getal toch priem is, dan hebben we een omkering van de stelling  van Fermat nodig. Hier doen zich twee moeilijkheden voor:

  • De directe omkering is gewoon fout! Het getal n = 1729 = 7.13.19 is niet priem en toch is  a^{1729}\equiv a \mod 1729 voor elk geheel getal a.
  • En zelfs al zou de omkering waar zijn, dan zou ons dat niet echt helpen want het is ondoenlijk alle gehele getallen a te proberen.

Het zoeken naar oplossingen van deze problemen is zeer actueel en de gevonden methoden zijn soms zelfs futuristisch, aangezien ze steunen op het nog onbewezen vermoeden betreffende de veralgemeende Riemannhypothese.  Enkele namen die op dit gebied een belangrijke bijdrage geleverd hebben zijn: R. Solovay, V.Strassen, G.L. Miller, M.O.Rabin en  H.W. Lenstra ( zie foto)

Fermat priemgetallen en regelmatige veelhoeken

Geplaatst op door

De Franse wiskundige Pierre de Fermat( 1601-1665) dacht dat alle getallen van de vorm 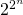2^{2^n} priemgetallen waren. En voor de eerste 5 waarden van n was dat ook zo:

\begin{array}{c|c} n& 2^{2^n} \\ \hline\\ 0 &3\\1&5\\2&17\\3&257\\4&65.537\end{array}

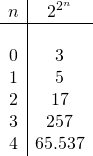
Later ontdekte Leonard Euler( 1707-1783) in 1732 dat het Fermat getal voor n = 5 ontbonden kon worden als  4.294.967.297 = 641 x 6.700.417. En hier zou het verhaal dan stoppen, ware er niet de geniale ontdekking van Carl Friedrich Gauss(1777-1855).

In 1794 vond Gauss dat een regelmatige veelhoek met p zijden (met p een priemgetal ) construeerbaar is met passer en liniaal als en slechts als p een Fermat priemgetal is, dus een priemgetal van de vorm 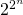2^{2^n}. Als eerbetoon werd in Brauschweig, de thuisstad van Gauss,  een bronzen standbeeld opgericht waar hij staat op een regelmatige zeventien hoek.

Welke regelmatige veelhoeken zijn dan construeerbaar met passer en liniaal? Volgens Gauss’ resultaat zijn dat de gelijkzijdige driehoek, de regelmatige 5-hoek, de regelmatige 17-hoek, de regelmatige 257-hoek en de  regelmatige 65.537-hoek. We weten dat ook de regelmatige veelhoeken met 7,11,13,19,… zijden niet construeerbaar zijn omdat het wel priemen zijn, maar geen Fermat priemen. Verder zijn ook regelmatige veelhoeken met 4,8,16,32,.. en 6,12,24,48,… zijden construeerbaar omdat we met passer en liniaal een hoek in twee kunnen verdelen. En wat met de anderen? Is een regelmatige 15 hoek construeerbaar?  Het blijkt van wel, omdat \frac{1}{15}=\frac{2}{5}-\frac{1}{3} en dus kunnen we een cirkel in 15 gelijke delen verdelen.

Het was uiteindelijk Pierre Wantzel die in 1837 volgend algemeen reultaat bewees: Een regelmatige n-hoek is construeerbaar met passer en liniaal als en slechts als n het product is van een macht van 2 en een willekeurig aantal verschillende Fermat priemgetallen.