Tag archieven: modulo rekenen

Opgave 43

Geplaatst op door

Een rij wordt gedefinieerd als : a_0=0 en a_{k+1}=3a_k+1. Toon aan dat a_{155} deelbaar is door 11.

Antwoord

  • We kunnen de eerste termen van de rij uitrekenen en proberen een regelmaat te vinden voor de termen die deelbaar zijn door 11. Dan kunnen we die regelmaat proberen te bewijzen, misschien wel via inductie.
  • Omdat het principe van deelbaarheid door 11 centraal staat is het misschien nuttiger de rij van de restklassen modulo 11 te berekenen.
  • Deze rij heeft als termen: 0,1,4,2,7,0,…. De rij moet zich wel herhalen na een eindig aantal stappen omdat er maar 11 mogelijke waarden zijn voor de restklassen. En inderdaad na 5 termen verschijn er terug een 0 en dus zal elke 5de term van de gegeven rij deelbaar zijn door 11. Bijgevolg is a_{155} deelbaar door 11.
  • We geven een Pythonprogramma als controle, waarbij we zelfs de 155ste term uitgerekend hebben:

Opgave 39

Geplaatst op door

Bewijs dat geen enkel getal van de vorm

    \[3^m+3^n+1\]

met m en n strikt positieve gehele getallen, een volkomen kwadraat is.

Antwoord

  • Veronderstel dat er toch een natuurlijk getal k bestaat zodat

        \[3^3+3^n+2=k^2\]

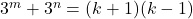  • Dan is 3^m+3^n=(k+1)(k-1). Omdat het linkerlid even is en omdat k-1 en k+1 dezelfde pariteit hebben, zijn k-1 en k+1 opeenvolgende even getallen.
  • Dit betekent ook dat ofwel k-1 ofwel k+1 een viervoud is. Het rechterlid (k-1)(k+1) is dus deelbaar door 8.
  • Bij deling door 8 zijn de resten van machten van 3 ofwel 1 ofwel 3. De som 3^m+3^n is dus modulo 8, gelijk aan 2,4 of 6 en dus zeker niet deelbaar door 8.
  • Bijgevolg kan 3^m+3^n+1 nooit een volkomen kwadraat zijn.

Op welk cijfer eindigt…

Geplaatst op door

Wat is de rest bij deling door 10 van het 2022ste getal in de rij  

    \[3,3^3,3^{3^3},...\]

  • De gegeven rij kan ook gegeven worden door middel van een recursief voorschrift: t_1=3 en t_{n+1}=3^{t_n}.

  • Berekenen we een paar termen van de rij: 3 , 27 , 7625597484987. We zien dat ze zeer snel toenemen in grootte, maar we hebben wel al 2 keer een 7 achteraan. Zou dat een patroon zijn?

  • Elke term is een viervoud plus 3, want t_n=(4 voud -1)^{t_{n-1}} en omdat elke term in de rij oneven is is t_n dus een 4voud min 1, of met anders geformuleerd : een drievoud plus 3.

  • Dan is t_{n+1}=3^{4v+3}=3^3.3^{4v}=27.81^v.
  • Werken we nu modulo 10: t_{n+1}\equiv 7.1^v\equiv 7.
  • Dus elke term van de rij eindigt op 7, dus ook de 2022ste term.

De klok

Geplaatst op door

Kunnen de drie wijzers van een uurwerk onderling twee aan twee hoeken van 120 graden vormen?

  • Noteer het tijdstip als x. Dit is een reëel getal. De kleine wijzer staat dan op 30x mod 360. graden, want na 1 uur heeft deze wijzer 30 graden afgelegd. De grote wijzer staat dan op 360x mod 360 graden, vermits er 60 minuten in een uur zijn. Omdat er 60 seconden in een minuut zijn , zal tenslotte de secondewijzer op 21600x mod 360 graden staan.
  • Het vraagstuk herleidt zich tot een volgend stelsel (telkens mod 360 genomen):

        \[30x-360x=120\]

        \[360x-21600x=120\]

        \[21600x-30x=120\]

  • Het kan ook het volgende  stelsel geven:

        \[360x - 30x=120\]

        \[21600x-360x=120\]

        \[30x-21600x=120\]

  • We bespreken enkel het eerste stelsel; het tweede geval verloopt analoog.
  • Na vereenvoudiging krijgen we :

        \[x=\frac{4}{11}(\mod \frac{12}{11})\]

        \[x=\frac{1}{177}(\mod \frac{3}{177})\]

        \[x=\frac{8}{719}(\mod \frac{12}{719})\]

  • Dus

        \[x=\frac{4}{11}(1+3k)=\frac{1}{177}(1+3l)=\frac{4}{719}(2+3m)\]

  • Maar dan moet  

        \[4.177.719(1+3k)=11.719(1+3l)\]

  • Dis  is onmogelijk want het eerste lid is een drievoud en het tweede niet!
  • De drie wijzers kunnen dus nooit twee aan twee een hoek van 120 graden vormen.