Overdekkingen van het vlak

Geplaatst op 27 augustus 2022 door admin

We gaan op zoek naar regelmatige bedekkingen van het vlak: dit zijn bedekkingen met regelmatige n-hoeken met alle dezelfde lengte als zijde. Het vlak is dan de unie van al die veelhoeken en de doorsnede van twee veelhoeken is ledig, ofwel een punt ofwel een zijde. We eisen ook dat de hoekpunten gelijkwaardig zijn, dus dat in een punt steeds dezelfde veelhoeken in dezelfde aantallen en in dezelfde volgorde voorkomen. Noteren we met $q$ het aantal verschillende veelhoeken in een bepaald knooppunt.

De waarde van een hoek van een regelmatige n-hoek is

$\frac{n-2}{n}180^{\circ}$

Neem eerst het geval $q=1$ . Noteer met m het aantal veelhoeken in een knooppunt. Dan moet $m.\frac{n-2}{n}180^{\circ}=360^{\circ}$ . Hieruit volgt dat $m(n-2)=2n$ of $(m-2)(n-2)=4$ . Hierbij zijn uiteraard m en n natuurlijke getallen. De enige oplossingen zijn:

$(m,n)=(6,3), (m,n)=(3,6), (m,n)=(4,4)$

Dus drie zeshoeken, zes driehoeken of vier vierkanten.

Neem nu $q=2$ ( we spreken dan van Archimedische vlakvullingen) en stel dat er a regelmatige m-hoeken en b regelmatige n-hoeken samenkomen, dan moet $a.\frac{m-2}{m}180^{\circ}+b.\frac{n-2}{n}180^{\circ}=360^{\circ}$ of

$a+b=2(\frac{a}{m}+\frac{b}{n}+1)$

Omdat $\frac{a}{m}+\frac{b}{n}>0$ zal $a+b\geq3$ . Omdat de klenst mogelijke hoek van een regelmatige veelhoek $60^{\circ}$ is, zal $a+b\leq 6$ . Bijgevolg geldt:

$3 \leq a+b \leq 6$

Geval 1: $a=1$ en $b=2$ , dan is $n=\frac{4m}{m-2}$ en zijn de enige natuurlijke oplossingen: $(m,n)=(3,12)$ en $(m,n)=(4,8)$ . De oplossing $(m,n)=(6,6)$ hebben we al en $(m,n)=(10,5)$ geeft geen regelmatige overdekking. De twee oplossingen geven we volgende typering: $3,12^2$ ( 1 driehoek en 2 twaalfhoeken) en $4,8^2$ (1 vierkant en 2 achthoeken).

Geval 2: $a=1$ en $b=3$ , dan is $n=\frac{3m}{3m-2}$ en is de enige natuurlijke oplossing: $(m,n)=(4,4)$ en die hebben we al gehad bij $q=1$ .

Geval 3: $a=1$ en $b=4$ , dan is $n=\frac{8m}{m-2}$ en zijn de enige natuurlijke oplossingen: $(m,n)=(6,3)$ . Typering: $6,3^4$ ( een zeshoek en 4 driehoeken)Geval 4: $a=2$ en $b=2$ , dan is $n=\frac{2m}{m-2}$ en zijn de enige natuurlijke oplossingen: $(m,n)=(3,6)$ , $(m,n)=(4,4)$ en $(m,n)=(6,3)$ . De oplossing $(m,n)=(4,4)$ hebben we al. Bovendien geven $(6,3)$ en $(3,6)$ dezelfde oplossing.Rest nog het geval $6^2,3^2$ (2 zeshoeken en 2 driehoeken).

Geval 5: $a=2$ en $b=3$ , dan is $n=\frac{6m}{3m-4}$ en is de enige natuurlijke oplossing: $(m,n)=(4,3)$ . Type $4^2,3^3$ ( twee vierkanten en drie driehoeken). We verfijnen de typering: links de overdekking $(3,3,3,4,4)$ en rechts $(3,3,4,3,4)$ .

Neem nu $q=3$ en stel dat er a regelmatige m-hoeken, b regelmatige n-hoeken en c regelmatige p-hoeken samenkomen, dan moet $a.\frac{m-2}{m}180^{\circ}+b.\frac{n-2}{n}180^{\circ}+c.\frac{p-2}{p}180^{\circ}=360^{\circ}$ of

$a+b+c=2(\frac{a}{m}+\frac{b}{n}+\frac{c}{p}+1)$

Waarbij $3\leq a+b+c<6$ zodat voor $(aub,c)$ volgende mogelijkheden moeten worden onderzocht: $(1,1,1),(2,1,1),3,1,1)$ en $(2,2,1)$ .

Geval 1: $(a,b,c)=(1,1,1)$ . Dan is $p=\frac{2mn}{mn-2m-2n}$ . Onderzoek van verschillende mogelijkheden geeft $(m,n,p)=(5,10,5),(5,20,4),(6,12,4),\\(8,8,4),(12,12,3),(15,10,3),(18,9,3),(24,8,3),(42,7,3)$ . Enkel $(m,n,p)=(6,12,4)$ levert een nieuwe bestaande overdekking. We krijgen een zeshoek, een twaalfhoek en een vierkant in elk knooppunt.

Geval 2: $(a,b,c)=(2,1,1)$ . Enkel $(m,n,p)=(4,6,3)$ levert een nieuwe bestaande overdekking. We krijgen twee vierkanten , een zeshoek en een driehoek in elk knooppunt. 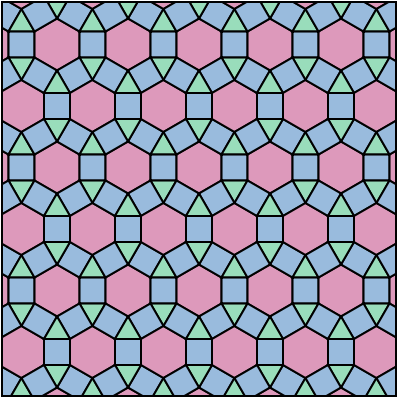Geval 3: $(a,b,c)=(3,1,1)$ . Deze combinatie levert geen nieuwe oplossingen.

Geval 4: $(a,b,c)=(2,2,1)$ . Deze combinatie levert geen nieuwe oplossingen.

Situaties met $q=4,5$ of $6$ kunnen niet voorkomen want $60+90+108+120=378>360$ .

Fermat priemgetallen en regelmatige veelhoeken

Geplaatst op 6 september 2018 door admin

De Franse wiskundige Pierre de Fermat( 1601-1665) dacht dat alle getallen van de vorm $2^{2^n}$ priemgetallen waren. En voor de eerste 5 waarden van n was dat ook zo:

$\begin{array}{c|c} n& 2^{2^n} \\ \hline\\ 0 &3\\1&5\\2&17\\3&257\\4&65.537\end{array}$

Later ontdekte Leonard Euler( 1707-1783) in 1732 dat het Fermat getal voor n = 5 ontbonden kon worden als 4.294.967.297 = 641 x 6.700.417. En hier zou het verhaal dan stoppen, ware er niet de geniale ontdekking van Carl Friedrich Gauss(1777-1855).

In 1794 vond Gauss dat een regelmatige veelhoek met p zijden (met p een priemgetal ) construeerbaar is met passer en liniaal als en slechts als p een Fermat priemgetal is, dus een priemgetal van de vorm $2^{2^n}$ . Als eerbetoon werd in Brauschweig, de thuisstad van Gauss, een bronzen standbeeld opgericht waar hij staat op een regelmatige zeventien hoek.

Welke regelmatige veelhoeken zijn dan construeerbaar met passer en liniaal? Volgens Gauss’ resultaat zijn dat de gelijkzijdige driehoek, de regelmatige 5-hoek, de regelmatige 17-hoek, de regelmatige 257-hoek en de regelmatige 65.537-hoek. We weten dat ook de regelmatige veelhoeken met 7,11,13,19,… zijden niet construeerbaar zijn omdat het wel priemen zijn, maar geen Fermat priemen. Verder zijn ook regelmatige veelhoeken met 4,8,16,32,.. en 6,12,24,48,… zijden construeerbaar omdat we met passer en liniaal een hoek in twee kunnen verdelen. En wat met de anderen? Is een regelmatige 15 hoek construeerbaar? Het blijkt van wel, omdat $\frac{1}{15}=\frac{2}{5}-\frac{1}{3}$ en dus kunnen we een cirkel in 15 gelijke delen verdelen.

Het was uiteindelijk Pierre Wantzel die in 1837 volgend algemeen reultaat bewees: Een regelmatige n-hoek is construeerbaar met passer en liniaal als en slechts als n het product is van een macht van 2 en een willekeurig aantal verschillende Fermat priemgetallen.

Veelhoeken ordenen

Geplaatst op 2 augustus 2015 door admin

Zes regelmatige veelhoeken zijn op volgorde in een band naast elkaar gezet, met een zijde op de onderkant. De bovenrand wordt beurtelings met een hoekpunt of met een hele zijde geraakt. Je zou kunnen zeggen dat de figuren dezelfde hoogte h hebben.

We vragen ons af : in welke volgorde moeten alle regelmatige veelhoeken
staan, gerangschikt naar hun oppervlakte? Lees hier de oplossing

Wiskunde is leuk

Tag archieven: regelmatige veelhoeken

Overdekkingen van het vlak

Fermat priemgetallen en regelmatige veelhoeken

Veelhoeken ordenen