matrix | Wiskunde is leuk

Noem $GL_n(F)$ de verzameling van alle n x n matrices over het veld F met een determinant die niet nul is. Het is duidelijk dat deze verzameling, uitgerust met de gewone matrixvermenigvuldiging, een groep is, want:

Omdat det( A.B)=det(A).det(B) zal 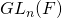$GL_n(F)$ gesloten zijn onder de vermenigvuldiging.
Omdat de determinant verschillend is van nul, heeft elke matrix een inverse.
De determinant van de eenheidsmatrix ( neutraal element) is verschillend van nul.

Een paar opmerkingen:

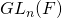$GL_n(F)$ is niet-abels voor elke 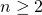$n\geq 2$ en voor elk veld F.
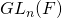$GL_n(F)$ is een eindige groep als en slechts als F een eindig veld is. Eindige velden zijn er voor elke waarde van p priem en voor alle priemmachten $p^m$ .
Als F een eindig aantal elementen q bezit, dan is het aantal elementen van 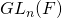$GL_n(F)$ gegeven door de formule
$(q^n-1)(q^n-q)\cdots(q^n-q^{n-1})$
Neem bijvoorbeeld $F=\mathbb{Z}_2$ , dan is de orden van $GL_2(\mathbb{Z}_2)$ gelijk aan 6. De enige niet-abelse groep van orde 6 is $S_3$ , dus is
$GL_2(\mathbb{Z}_2) \cong S_3$

Een ander ‘leuk’ voorbeeld is de Heisenberg groep H(F), vernoemd naar de Duitse natuurkundige Werner Heisenberg( 1901-1976).

H(F) bevat alle 3 x 3 bovendriehoeksmatrices van de vorm

$\begin{pmatrix} 1&a&b\\0&1&c\\0&0&1\end{pmatrix}$

Het is duidelijk dat deze matrices allen een determinant gelijk aan 1 hebben, dus is H(F) een deelgroep van $GL_3(F)$ . Neem voor F een eindig veld met q elementen , dan zien we dat de orde van H(F) gelijk is aan $q^3$ .

Bekijken we even de situatie als $F=\mathbb{Z}_2$ , dan telt H(F) dus 8 elementen. Er zijn 5 elementen van orde 2, zoals bijvoorbeeld $\begin{pmatrix} 1&1&0\\0&1&0\\0&0&1\end{pmatrix}$ en 2 elementen van orde 4, zoals bijvoorbeeld $\begin{pmatrix} 1&1&0\\0&1&1\\0&0&1\end{pmatrix}$ . Bijgevolg is

$H(\mathbb{Z}_2)\cong D_4$

Een tovervierkant is een vierkantig rooster van getallen zodat de som van de elementen op elke rij, kolom en diagonaal hetzelfde is. Het oudste tovervierkant wordt toegeschreven aan Lo Shu en dateert van omstreeks 2200 voor onze tijdrekening. Hij was gekerfd in het schild van een schildpad in de Lo-rovier.

Of in matrixvorm :

Als we deze matrix L noemen , kunnen we ook L² en L³ uitrekenen:

$L^2 =\begin{pmatrix} 59&83&83\\83&59&83\\83&83&59\end{pmatrix}$

$L^3=\begin{pmatrix}1149&1029&1197\\1173&1125&1077\\1053&1221&1101\end{pmatrix}$

De matrix $L^2$ is symmetrisch en is een pseudo-tovervierkant ( de som van de elementen op elke rij en in elke kolom is dezelfde; de sommen van de diagonalen echter niet ).

De matrix $L^3$ is dan weer wel een tovervierkant, maar de symmetrie is verdwenen.

Wiskunde is leuk

Tag archieven: matrix

Matrixgroepen

Het tovervierkant van Lo Shu