Neem 2 geordende n-tallen ![]() en
en ![]() . Als
. Als ![]() ,
, ![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() en
en ![]() , dan zeggen we dat het n-tal
, dan zeggen we dat het n-tal ![]() het n-tal
het n-tal ![]() majorizeert en we noteren
majorizeert en we noteren ![]() .
.
Dit gaan we gebruiken in volgende stelling over ongelijkheden:
Als f een convexe functie is op een interval I en ![]() met
met ![]() , dan zal
, dan zal
![]()
- Als f strikt convex is krijg je een gelijkheid als en slechts als
 .
. - Er is een gelijkaardig resultaat voor concave functies, als je de ongelijkheidstekens omdraait.
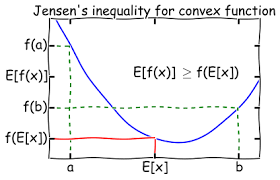
- Deze stelling is een veralgemening van de ongelijkheid van Jensen, waarbij
 . Hierbij is x het rekenkundig gemiddelde van de getallen
. Hierbij is x het rekenkundig gemiddelde van de getallen  .
.
Een voorbeeld:
Vind de maximum waarde van ![]() als
als ![]() en
en ![]() .
.
- De functie
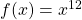 is convex op
is convex op ![Rendered by QuickLaTeX.com \left[-1,1\right]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-6bcea056f0fffaa9cb906f003ea1de6b_l3.png?media=1678572382) , want
, want  op
op ![Rendered by QuickLaTeX.com \left[-1,1\right]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-6bcea056f0fffaa9cb906f003ea1de6b_l3.png?media=1678572382) .
. - Veronderstel
 .
. - Dan is
 , want eerst en vooral is
, want eerst en vooral is  . Verder is
. Verder is  , dus is
, dus is  .
. - Volgens de majorisatie ongelijkheid is dan
 .
. - De maximumwaarde van
 wordt bereikt voor
wordt bereikt voor 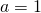 ,
, 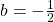 en
en  .
.