Voor 3 positieve getallen a,b en c geldt:

$\frac{9}{2(a+b+c)}\leq \frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{a+c}\leq \frac{1}{2}\Big(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\Big)$

Antwoord

In de eerste ongelijkheid stellen we 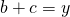$a+b=x$ , $b+c=y$ en $a+c=z$ , dan wordt de opgave herschreven als $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\geq \frac{9}{x+y+z}$ of $(x+y+z)\Big( \frac{1}{x}+\frac{1}{y}+\frac{1}{z}\Big )\geq 9$ .
We werken de haakjes uit en vinden: $3+\Big( \frac{x}{y}+\frac{y}{x}\Big)+\Big( \frac{x}{z}+\frac{z}{x}\Big)+\Big( \frac{y}{z}+\frac{z}{y}\Big) \geq 9$ .
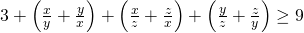Uit de ongelijkheid over het rekenkundig en meetkundig gemiddelde vinden we dat $\frac{1}{2}\Big( \frac{x}{y}+\frac{y}{x}\Big) \geq \sqrtç \frac{x}{y}\frac{y}{x}=1$ , dus het linkerlid uit vorig punt is groter of gelijk aan $3+2+2+2=9$ wat moest bewezen worden.
Voor het tweede deel van de ongelijkheid gebruiken we de ongelijkheid over het harmonisch en meetkundig gemiddelde: 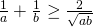$\frac{1}{a}+\frac{1}{b} \geq \frac{2}{\sqrt{ab}}$ . Volgens de ongelijkheid over het rekenkundig en meetkundig gemiddelde is bovendien $\frac{2}{\sqrt{ab}} \geq \frac{4}{a+b}$ .
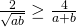Pas dit nu toe op de drie termen van het linkerlid van de gevraagde ongelijkheid en het bewijs is klaar.