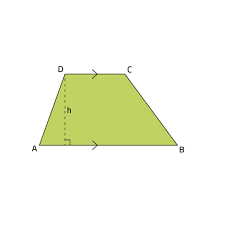
 Lees in dit artikel hoe je in een trapezium het rekenkundig, het meetkundig, het harmonisch en het kwadratisch gemiddelde kan terugvinden.
Lees in dit artikel hoe je in een trapezium het rekenkundig, het meetkundig, het harmonisch en het kwadratisch gemiddelde kan terugvinden.

 Lees in dit artikel hoe je in een trapezium het rekenkundig, het meetkundig, het harmonisch en het kwadratisch gemiddelde kan terugvinden.
Lees in dit artikel hoe je in een trapezium het rekenkundig, het meetkundig, het harmonisch en het kwadratisch gemiddelde kan terugvinden.
De vraag die we willen behandelen in deze tekst luidt:
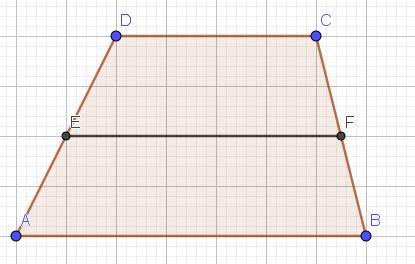
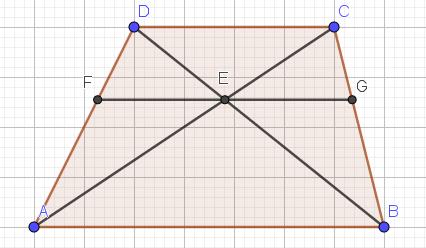 Uit de gelijkvormigheid van de driehoeken FDE en ADB, CEG en CAB, DEC en EAB volgt dat
Uit de gelijkvormigheid van de driehoeken FDE en ADB, CEG en CAB, DEC en EAB volgt dat 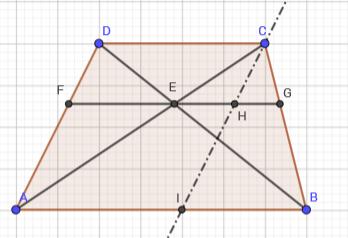 Nu is
Nu is
![]()
Neem n positieve getallen ![]() . Dan definieren we:
. Dan definieren we:
Als ![]() , dan geldt volgende ongelijkheid:
, dan geldt volgende ongelijkheid:
![]()
De gelijkheid krijgen we als ![]() .
.
Voor twee positieve getallen ![]() en
en ![]() vinden we zo:
vinden we zo:
![]()