Velduitbreidingen
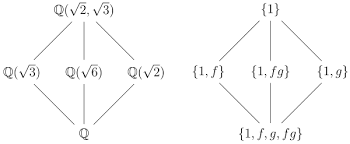
In deze tekst kan je een inleiding vinden tot velduitbreidingen , ontbindingsvelden en de Galois groep van een velduitbreiding.
Galois
Elementaire symmetrische functies
Kunnen we elke symmetrische uitdrukking van de n oplossingen van een n de graads veeltermvergelijking uitdrukken in functie van de coëfficiënten van de gegeven vergelijking? Voor een tweedegraads vergelijking lukt dat . Maar hoe zit dat met een hogere graad. Lees hiervoor volgend artikel. Hiermee komen we terecht in het werk van E. Galois , … Lees verder
Evariste Galois
Galoistheorie, genoemd naar Evariste Galois, geeft een link tussen problemen in lichamentheorie en groepentheorie. Oorspronkelijk gebruikte Galois permutatiegroepen voor het beschrijven van de relaties tussen verschillende wortels van een veelterm vergelijking. De oorspronkelijke motivatie voor Galois theorie was de volgende vraag: “Waarom is er geen formule voor de wortels van een 5de graads (of hogere graad) veelterm, … Lees verder