Bereken de som van de coëfficiënten van de veelterm P(x) als
![]()
- Het is handig te weten dat de som van de coëfficiënten van een veelterm kan berekend worden door de getalwaarde van 1 te berekenen, dus
 .
. - Vullen we 1 in bij de gegeven identiteit, dan vinden we:
 ;
; - Hieruit volgt dat
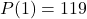
- De som van de coëfficiënten van de veelterm Px) is dus 119.

![Rendered by QuickLaTeX.com \[D_k(x)=\sum_{i=0}^k\binom{k}{i}P(x+i)\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-3f5b7917e846a456af91f1b79ca2c842_l3.png?media=1678572382)


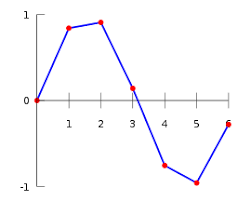

![Rendered by QuickLaTeX.com \[f(n+1)=\sum_{k=0}^n(-1)^{n-k}\frac{(n+1)!}{(k+1)!(n-k)!}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-5f36c4aae7691b7a6e4ddf6bfe1c965b_l3.png?media=1678572382)
![Rendered by QuickLaTeX.com \[f(n+1)=\sum_{l=1}^{n+1}(-1)^{n-l+1}\frac{(n+1)!}{l!(n+1-l)!}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-ab304002d0efcf854047e5f69d66ecb2_l3.png?media=1678572382)

