antwoord
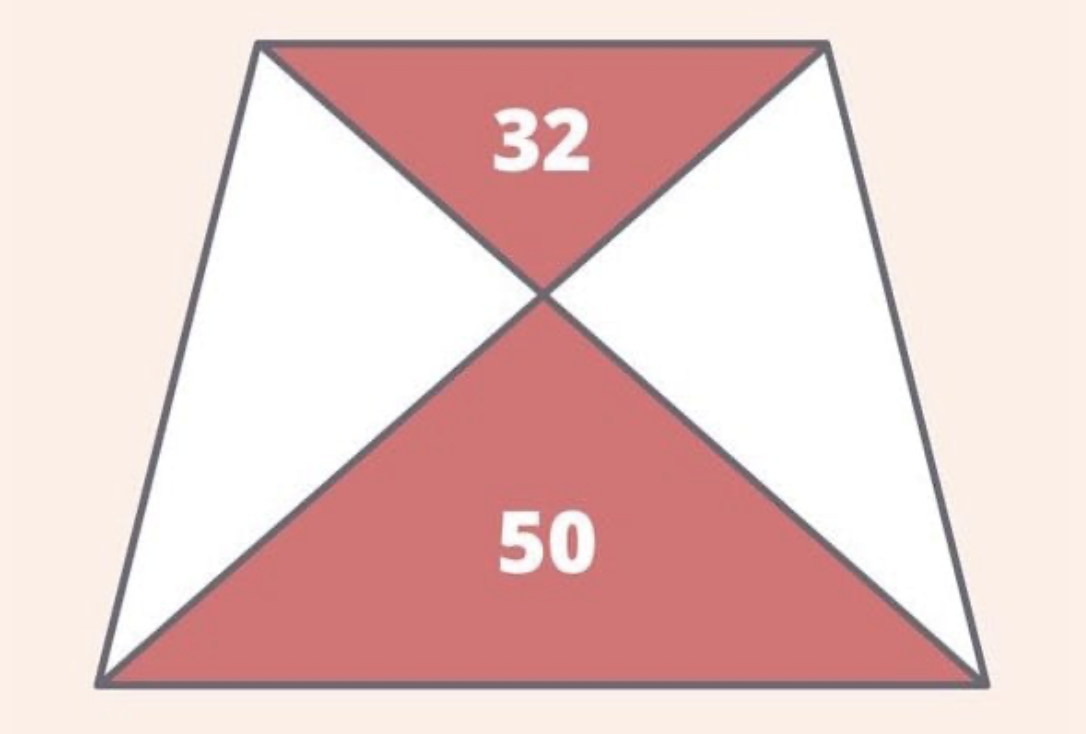
- Gevraagd wordt de totale oppervlakte vanher trapezium te berekenen.
- De driehoeken met gegeven oppervlakten 32 en 50 zijn gelijkvormig. Hun oppervlakten verhouden zich als het kwadraat van de gelijkvormigheidsfactor. Bijgevolg is de gelijkvorrmgheidsfactor
![\[r=\frac{4}{5}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-45ffe6a4a03f6db616862b1c12353343_l3.png?media=1678572382 "Rendered by QuickLaTeX.com")
- Noteer dan
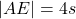en 
. Analoog 
en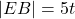 
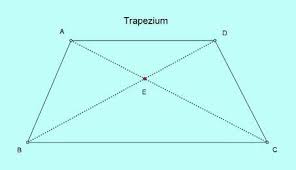
. - De 4 hoeken in E hebben allemaal eenzelfde sinus als overstaande hoeken of supplementaire hoeken. Noteer deze sinus door x.
- Om de oppervlakte van een driehoek te berekenen, gebruiken we de formule: de helft van het product van twee zijden , vermenigvuldigd met de sinus van de ingesloten hoek.
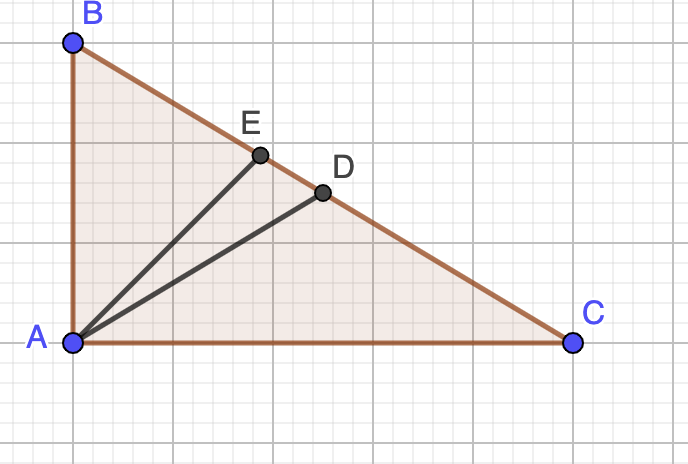
- Oppervlakte ADE=
. Dus is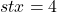 
. - De oppervlakte van AEB=
Analoog is ook de oppervlakte van driehoek DEC gelijk aan 40. - De totale oppervlakte is dan 32 + 50 + 40 + 40 = 162.
en als hoogte 
. De gevraagde oppervlakte bedraagt dus 3 oppervlakte eenheden.
.
.
.
, met c de schuine zijde. Maar de zwaartelijn getrokken naar de schuine zijde is gelijk aan de helft van die schuine zijde. Dus 
.
gelijk aan het dubbele van de oppervlakte van de driehoek, dus 
.
.
.![\[A=\frac{x^2+x\sqrt{x^2+8y^2}}{4}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-62ed6e76d59f6b71e4981024e29c7492_l3.png?media=1678572382 "Rendered by QuickLaTeX.com")
