Tag archieven: problem solving

Opgave 35

Geplaatst op door

N is een natuurlijk getal. Een goede verdeling van N is een partitie van \{1,2,\cdots,N\} in twee gescheiden, niet lege deelverzamelingen S_1 en S_2, zo dat de som van de elementen van S_1 gelijk is aan het product van de elementen van S_2. Bewijs dat voor N\geq 5 er altijd een goede verdeling bestaat.

Spoiler

Nootje 27

Geplaatst op door

 

 

 

Spoiler

Op welk cijfer eindigt…

Geplaatst op door

Wat is de rest bij deling door 10 van het 2022ste getal in de rij  

    \[3,3^3,3^{3^3},...\]

  • De gegeven rij kan ook gegeven worden door middel van een recursief voorschrift: t_1=3 en t_{n+1}=3^{t_n}.

  • Berekenen we een paar termen van de rij: 3 , 27 , 7625597484987. We zien dat ze zeer snel toenemen in grootte, maar we hebben wel al 2 keer een 7 achteraan. Zou dat een patroon zijn?

  • Elke term is een viervoud plus 3, want 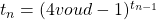t_n=(4 voud -1)^{t_{n-1}} en omdat elke term in de rij oneven is is t_n dus een 4voud min 1, of met anders geformuleerd : een drievoud plus 3.

  • Dan is t_{n+1}=3^{4v+3}=3^3.3^{4v}=27.81^v.
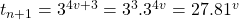  • Werken we nu modulo 10: t_{n+1}\equiv 7.1^v\equiv 7.
  • Dus elke term van de rij eindigt op 7, dus ook de 2022ste term.

Nog 2 opgaven over priemgetallen

Geplaatst op door

De som van twee tweelingpriemen, groter dan 3, is deelbaar door 12.

Antwoord

Veronderstel dat p een priemgetal is en dat allebei de oplossingen van x^2+px-444p=0 gehele getallen zijn, zoek dan de mogelijke waarden van p.

 

Antwoord