februari | 2016 | Wiskunde is leuk

Gegeven zijn 2 natuurlijke getallen $a$ en $b$ . Het grootste natuurlijk getal dat zowel een deler is van $a$ als van $b$ heet de grootste gemene deler van $a$ en $b$ . Notatie : ggd[a,b). Het kleinste getal dat zowel een veelvoud is van $a$ als van $b$ , heet het kleinste gemene veelvoud van $a$ en $b$ . Notatie : kgv(a,b).

Men kan de grootste gemene deler en het kleinste gemene veelvoud van 2 getallen bepalen door beide getallen te ontbinden in priemfactoren. Vooral bij grotere getallen kan dit een omvangrijk werk zijn. Er is een veel snellere methode. Deze berust op de eigenschap dat als $b=q.a+r$ , dan geldt er dat ggd (a,b) = ggd(a,r). Elke deler van $a$ en $b$ is immers ook een deler van $r=b-q.a$ en omgekeerd elke deler van $a$ en $r$ is ook een deler van $b$ . Deze werkwijze noemt men het algoritme van Euclides.

We berekenen de ggd van 1970 en 1066 op twee manieren:

1970 = 2.5.197 en 1066 = 2.13.41, dus is ggd(1970,1066)=2
1970 = 1.1066 + 904 ; 1066=1.904+162 ; 904=5.162+94 ; 162=1.94+68 ; 94=1.68+26 ; 68=2.26+16 ; 26=1.16+10 ; 16=1.10+6 ; 10=1.6+4 ; 6=1.4+2 ; 4=2.2. Dus is ggd(1970,1066)=ggd(1066,904)=ggd(904,162)=ggd(162,94)=ggd(94,68) = ggd(68,26)=ggd(26,16)=ggd(16,10)=ggd(10,6)=ggd(6,4)=ggd(4,2)=2

Via dit algoritme kan men ( zoals hieronder in de stelling van Bezout vermeld wordt) de grootste gemene deler van 2 getallen schrijven als een lineaire combinatie van die twee getallen.
ggd(1970,1066)= 2= 6 – 4 = 6 – (10 – 6) = 2.6 – 10 = 2.(16 – 10) – 10 = 2.16 – 3.10 = $\ldots$ = 377.1066 – 204.1970.

Enkele eigenschappen

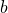Elke gemeenschappelijke deler van $a$ en $b$ is ook een deler van ggd(a,b)
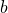Elk gemeenschappelijk veelvoud van $a$ en $b$ is ook een veelvoud van kgv(a,b).
ggd(a,b).kgv(a,b)=a.b
Als 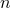$n$ een deler is van 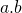$a.b$ en als ggd(n,a) = 1 dan moet 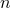$n$ een deler zijn van $b$ .
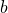Als ggd(a,b)=d dan geldt : ggd( 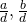$\frac{a}{d},\frac{b}{d}$ )=1
ggd(a,b) = ggd(b,a – qb)
De grootste gemene deler van 2 getallen is een lineaire combinatie van die twee getallen ( stelling van Bezout ).

Elk samengesteld getal kan geschreven worden als het product van kleinere factoren. Als minstens 1 van beide samengesteld is , kan men die ook weer schrijven als product van kleinere factoren. Zo kan men doorgaan tot er slechts priemgetallen als factoren overblijven. men kan een samengesteld getal in het algemeen op verschillende manieren via een aantal tussenstappen in priemgetallen ontbinden. Het uiteindelijk resultaat, de ontbinding in priemfactoren, is steeds hetzelfde. Dit resultaat staat bekend als de hoofdstelling van de rekenkunde:

$\begin{center}De ontbinding in priemfactoren van een \\ natuurlijk getal is eenduidig bepaald.\end{center}$

Deze eigenschap is in andere getalsysytemen niet noodzakelijk waar. Beschouw de verzameling van de even getallen $\left\{2,4,6,\cdots \right\}$ . Sommige ervan kan men schrijven als het product van even factoren, bijvoorbeeld $20=2.10$ . Bij andere is dat niet mogelijk. We noemen even getallen die niet het product zijn van even factoren even-priemgetallen. Een even getal is te schrijven als product van even-priemgetallen, maar zo een ontbinding hoeft niet eenduidig te zijn. Zo is $420=6.70=10.42$

Als een getal ontbonden is in priemfactoren, dan kan men het aantal delers bepalen. Stel dat $n=2^{e_1}.3^{e_2}.5^{e_3}. \ldots .p_k^{e_k}$ dan heeft $n$ juist $(e_1+1)(e_2+1)(e_3+1).\ldots.(e_k+1)$ delers.

Wiskunde is leuk

Maandelijks archief: februari 2016

GGD en KGV

Hoofdstelling van de rekenkunde