Categorie archieven: Geen categorie

Nog 5 haiku’s

Geplaatst op door

Nu het verbeteren achter de rug is , de laatste haiku’s van het jaar , in volgorde  gemaakt door Toon Wielemans, Victor Peuters, Iben Eembeeck, Tristan Boschman en Mateja Marcos/

breuk van sin op cos

tussen nul en oneindig

gelijk aan rico

 

algebra fluistert

onbekende letter staat

de oplossing wacht

snijdende rechten

komen samen in één punt

dan gewoon verder

getal na getal

verschillen en producten

oplossing verschijnt

even spiegelt mooi

oneven doet dat door nul

symmetrie doet mee

Nootje 52

Geplaatst op door

Een bol is ingeschreven in een afgeknotte kegel en het volume van de bol is de helft van het volume van de afgeknotte kegel. Bereken de verhouding van de stralen van boven en ondervlak van die afgeknotte kegel.

Antwoord

  • We zoeken de verhouding \frac{b}{a}.
  • De blauwe lijnstukken zijn gelijk als ook de rode omdat raaklijnen uit een punt buiten de cirkel evenlaag zijn.
  • De groene driehoek is rechthoekig omdat de rechthoekzijde de bissectrices zijn van twee supplementaire hoeken. Dus is ab=r^2.
  • Volume bol is \frac{4}{3}\pi r^3 en het volume van de afgeknotte kegel = \frac{1}{3}h\pi(a^2+ab+b^2).
  • Omdat de hoogte van de afgeknotte gele gelijk is aan 2r en omdat het volume van de bol de helft is van die van de afgeknotte kegel is

        \[\frac{4}{3}\pi r^3=\frac{1}{2}\frac{1}{3}2r\pi (a^2+ab+b^2)\]

    .
  • Hieruit volgt: 4r^2=a^2+ab+b^2; Maar r^2=ab, dus is a^2-3ab+b^2=0.
  • Stel de verhouding \frac{b}{a}=x, dan is x^2-3x+1=0.
  • Het oplossen van deze vierkantsvergelijking geeft x=\frac{3\pm \sqrt{5}}{2}.
  • Omdat b>a vinden we uiteindelijk dat

        \[x=\frac{3+\sqrt{5}}{2}\]

Minoïsche beschaving

Geplaatst op door

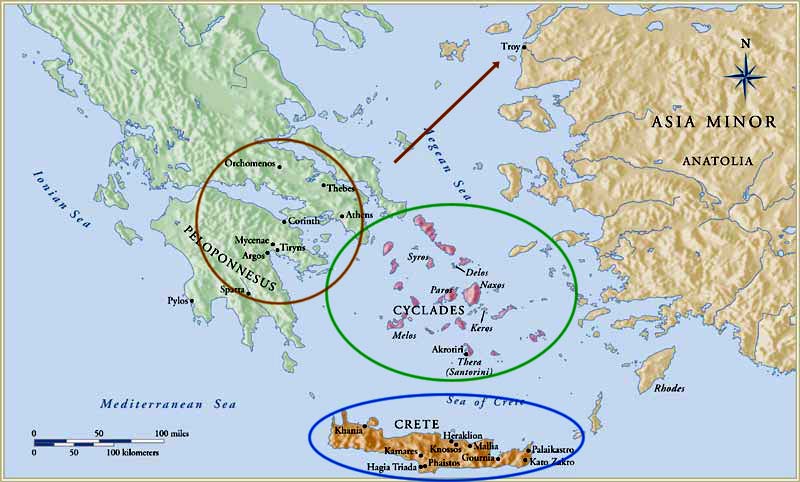
De Minoïsche beschaving, genoemd naar de legendarische koning Minos, was een oude beschaving die bloeide op het eiland Kreta in de Egeïsche Zee tijdens het bronzen tijdperk, van ongeveer 2700 tot 1450 v.Chr. Het was een van de eerste geavanceerde beschavingen in Europa en wordt beschouwd als een cruciale periode in de prehistorische tijd van de Egeïsche regio.

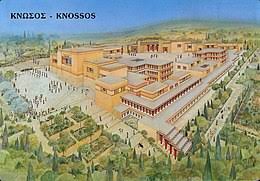
De Minoïsche beschaving wordt geassocieerd met de bouw van grote paleizen, waarvan het paleis van Knossos het meest bekende is. Deze paleizen waren niet alleen administratieve en politieke centra, maar ook culturele en religieuze centra. Ze waren vaak complex van structuur, met vele kamers, gangen en binnenplaatsen. Rond 1700 v.C. werd Kreta getroffen door een natuurramp. Kolonisten van Indo-Europese afkomst zetten voet op het eiland. Daarna werden nieuwe Minoïsche paleizen gebouwd. Na een nieuwe natuurramp rond 1450 v.C.  vallen de verwoeste paleizen in handen van de Myceense Grieken. Zij zijn de nieuwe heersers in de regio. 

De Minoërs waren bedreven in handel en onderhielden uitgebreide handelsnetwerken met andere culturen in de Egeïsche Zee, Egypte en het Nabije Oosten. Ze waren vooral bekend om hun handel in luxegoederen zoals aardewerk, edelstenen, wierook en grondstoffen zoals koper. Een onmisbaar element hierbij is de opkomst van het schrift: Lineair A.  Het bestaat uit pictogrammen en de taal die deze tekens weergeven is tot op heden niet ontcijferd

 

De Minoïsche beschaving stond bekend om zijn uitgebreide artistieke en ambachtelijke tradities. Minoïsche kunst omvatte prachtige fresco’s, aardewerk, juwelen en sculpturen. Veel van deze kunstwerken vertoonden thema’s van de natuur, dieren, en religieuze rituelen.

 De Minoïsche religie en symboliek zijn slecht begrepen vanwege het ontbreken van geschreven verslagen. Veel van wat we weten is afgeleid van archeologische vondsten, zoals de aanwezigheid van goden en godinnen, waaronder de bekende slangengodin. Symbolen zoals de dubbele bijl (labrys) en stieren speelden een belangrijke rol in hun religieuze praktijken.

 De Minoïsche beschaving kende een plotselinge en mysterieuze ondergang rond 1450 v.Chr., waarschijnlijk als gevolg van een combinatie van natuurrampen, waaronder aardbevingen en de uitbarsting van de vulkaan Thera (Santorini), evenals mogelijk invasies van buitenaf, hoewel de precieze oorzaak nog steeds onderwerp van debat is onder historici en archeologen.

Ondanks zijn ondergang heeft de Minoïsche beschaving een blijvende invloed gehad op de Griekse cultuur en beschaving, en het eiland Kreta blijft een belangrijke archeologische vindplaats voor het bestuderen van deze oude beschaving.

Basisfeiten over groepen

Geplaatst op door

Voor de classificatie van eindige groepen kunnen we beroep doen op de stellingen van Sylow ofwel kunnen we gebruik maken van een aantal elementaire eigenschappen:

  • Groepen van priem orde  zijn cyclisch en uniek op een isomorfisme na.
  • Toegevoegde elementen hebben dezelfde orde.
  • Als de quotiënt groep van G met zijn centrum Z(G) cyclisch is, dan is G abels.
  • Als in een groep G, alle elementen, behalve het eenheid element, orde 2 hebben, dan is G abels.
  • Als p priem is, dan is het aantal elementen van orde p altijd een veelvoud van p – 1.
  • Als een groep G gegenereerd wordt door 2 normale deelgroepen H en K ( dus elk element van G is te schrijven onder de vorm h_1k_1h_2k_2...h_rk_r, en als H\capK=\{e\} dan is G het direct product van H met K. Dus  G\cong H \times K.
  • Abelse groepen zijn ofwel cyclisch ofwel het direct product van cyclische groepen.