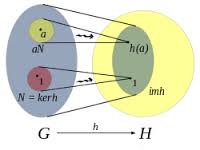
Bewijs dat voor alle positieve 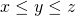 geldt dat
geldt dat
![]()
- Als
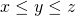 , dan is
, dan is 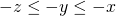 . Door overal
. Door overal 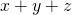 op te tellen vinden we dan dat
op te tellen vinden we dan dat 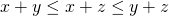 en
en 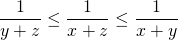 .
. - Door de ongelijkheden
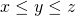 en
en 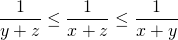 lid per lid te vermenigvuldigen ( getallen zijn allemaal positief) krijgen we :
lid per lid te vermenigvuldigen ( getallen zijn allemaal positief) krijgen we : 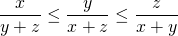 .
. - Dan zijn
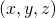 en
en 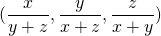 gelijk geordend.
gelijk geordend. - Gebruik van de herschikkingsongelijkheid geeft de oplossing.