Maandelijks archief: augustus 2019

Telescopische som

Geplaatst op door

Eén van de technieken bij problem-solving bestaat eruit het probleem van een andere kant te bekijken of een eenvoudiger probleem te nemen. Illustreren we dit even met volgend probleem: Vereenvoudig:

    \[\sum_{n=1}^{2020}\tan n\tan(n+1)\]

  • We gaan het product herschrijven als een som zodat bij het sommeren van al die termen ze één voor één tegen elkaar wegvallen , op de eerste en laatste na.
  • Gebruik hiervoor de formule voor het berekenen van de tangens van een verschil: \tan((n+1)-n)=\tan 1=\frac{\tan(n+1)-\tan n}{1+\tan(n+1)\tan n}.
  • Hieruit volgt dat \tan n\tan(n+1)=\frac{\tan (n+1)-\tan n }{\tan 1}-1
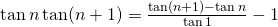
  • Invullen in de opgave geeft :

        \[\frac{\tan 2021-\tan 1}{\tan 1}-2020=\frac{\tan 2021}{\tan 1}-2021\]

Zuid-Afrikaanse wiskundeolympiade

Geplaatst op door

In Zuid-Afrika is men zich bewust dat de welvaart van Zuid-Afrika mede bepaald wordt door hoog gekwalificeerd wiskunde personeel.  Twee organisaties SAMS ( South African Mathematical Society) en Amesa (Association for Mathematics Education of South Africa) besloten hun krachten te bundelen op het gebied van wiskunde ontwikkeling en onderwijs. Zo werd in 2004 de SAMF (South African Mathematical Foundation) opgericht. Het kantoor wordt aangedreven door een uitstekend team van professionals die samenwerken met de overheid, scholen en andere belanghebbenden om het wiskundeonderwijs in Zuid-Afrika te verbeteren. Op hun website   vindt je  info  over de Zuid-Afrikaans wiskunde olympiade en andere competities of trainingsmateriaal.

Tekenregel van Descartes

Geplaatst op door

De tekenregel werd voor het eerst genoemd in het werk ‘La géometrie’ van René Descartes (1596-1650). Het gaat over veeltermen met reële coëfficiënten en we zijn geïnteresseerd in het aantal positieve nulwaarden. Veronderstellen we voor de rest van deze tekst dat de coëfficiënt van x^n gelijk is aan 1, dat de constante term niet nul is  en dat de veelterm geordend is naar afnemende machten van x.

Het fundamenteel theorema van de algebra zegt dat een veelterm van graad n steeds n nulwaarden heeft in \mathbb{C}. Meestal zijn we niet in staat deze nulwaarden te vinden. Toch kunnen we informatie vinden over het aantal positieve reële nulwaarden ( p) en het aantal negatieve nulwaarden (n). Bestudeer hiervoor het aantal teken veranderingen in de rij van tekens van de niet nul zijnde coëfficiënten van de gegeven veelterm P(x):

  • De waarde p heeft dezelfde pariteit als het aantal  tekenveranderingen.
  • De waarde p is kleiner of gelijk aan het aantal tekenveranderingen.
  • Om n te bepalen bepalen we p voor de veelterm P(-x).

Een voorbeeld: P(x)=x^6-6x^5+10x^4-2x^3-3x^2+4x-12.

  • Er zijn 5 tekenveranderingen.
  • p\leq 5 en p is oneven, dus p = 1, 3 of 5
  • P(-x)=x^6+6x^5+10x^4+2x^3-3x^2-4x-12. Er is 1 tekenverandering dus n=1.
  • Narekenen geeft als nulwaarden: -1 en 2 met multipliciteit 2 en 3.

De stelling van Napoleon

Geplaatst op door

Iedereen kent gelijkvormige driehoeken. In deze tekst proberen we ze te beschrijven met complexe getallen. Elk punt Z in het vlak correspondeert met een uniek complex getal z.

Twee driehoeken ABC en DEF zijn rechtstreeks gelijkvormig ( alle  hoeken hebben eenzelfde oriëntatie, bvb met de klok mee) als en slechts als

    \[\begin{vmatrix} a&d&1\\b&e&1\\c&f&1 \end{vmatrix}=0\]

Bij onrechtstreekse gelijkvormigheid moet je , in de tweede kolom, elk complex getal vervangen door zijn complex toegevoegde. Gebruiken we deze formules nu op een voorbeeld:

De stelling van Napoleon luidt dat als aan de zijden van een willekeurige driehoek gelijkzijdige driehoeken worden vastgemaakt, ofwel alle drie naar buiten, ofwel naar binnen gericht, dat vormen de zwaartepunten van die driehoeken  een gelijkzijdige driehoek.

  • We veronderstellen alle driehoeken klok georiënteerd.
  • Elke gelijkzijdige driehoek is gelijkvormig met de driehoek gevormd door de complexe getallen 1,\omega en \omega^2 . Hierbij is \omega=\frac{-1+\sqrt{3}i}{2}.
  • Als ABC gelijkzijdig is dan moet

        \[a+b\omega+c\omega^2=0\]

    Dit volgt uit vorige opmerking.

  • Dus is :

        \[\begin{array}{c} c+x\omega+b\omega^2=0\\b+z\omega+a\omega^2=0\\a+y\omega+c\omega^2=0\end{array}\]

  • Door de tweede vergelijking te vermenigvuldigen met \omega en de derde met \omega^2 vinden we:

        \[\begin{array}{c} c+x\omega+b\omega^2=0\\a+b\omega+z\omega^2=0\\y+c\omega+a\omega^2=0\end{array}\]

  • Omdat M,L en N zwaartepunten zijn geldt: m=\frac{a+c+y}{3},l=\frac{c+x+b}{3} en n=\frac{a+b+z}{3}.
  • Rest ons te bewijzen dat MLN gelijkzijdig is, daartoe moeten we bewijzen dat m+l\omega+n\omega^2=0. Een combinatie van de twee laatste puntjes geeft ons het gewenste resultaat.

Goniometrische substituties

Geplaatst op door

We kennen het gebruik van een goniometrische substitutie bij het berekenen van onbepaalde integralen. Maar ze kunnen ook hun nut hebben bij de studie van ongelijkheden. Een voorbeeld:

Als a,b,c,en d positieve reële getallen zijn en

    \[\frac{1}{1+a^4}+\frac{1}{1+b^4}+\frac{1}{1+c^4}+\frac{1}{1+d^4}=1\]

bewijs dan dat abcd \geq 3.

  • Stel a^2=\tan x, b^2=\tan y,c^2=\tan z en d^2=\tan t
  • Omdat 1+\tan^2x=\frac{1}{\cos^2x} wordt de gegeven ongelijkheid: \cos^2x+\cos^2y+\cos^2z+\cos^2t=1
  • We gebruiken nu de ongelijkheid van het rekenkundig en meetkundig gemiddelde: \sin^2x=1-\cos^2x=\cos^2y\cos^2z\cos^2t \geq 3(\cos y.\cos z.\cos t)^{\frac{2}{3}}
  • Analoog \sin^2y\geq 3(\cos x.\cos z.\cos t)^{\frac{2}{3}}.
  • Of \sin^2z\geq 3(\cos x.\cos y.\cos t)^{\frac{2}{3}}.
  • En \sin^2t\geq 3(\cos x.\cos y.\cos z)^{\frac{2}{3}}.
  • Als we nu deze 4 ongelijkheden met elkaar vermenigvuldigen vinden we dat \sin^2x.\sin^2y.\sin^2z.\sin^2t \geq 81 \cos^2x.\cos^2y.\cos^2z.\cos^2t.
  • Hieruit volgt dat \tan^2x.\tan^2y.\tan^2z.\tan^2t \geq 81 of a^4b^4c^4d^4 \geq 81.
  • Omdat a,b,c en d positief zijn volgt hieruit dat abcd \geq 3.