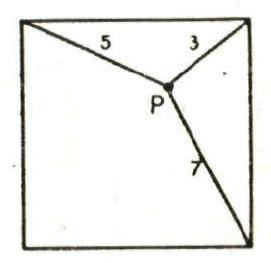
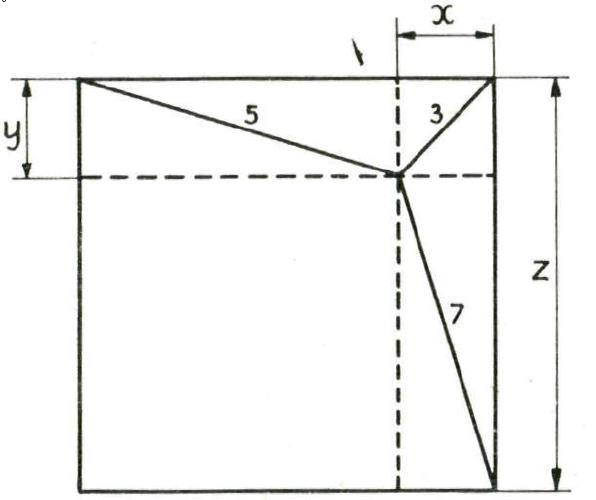
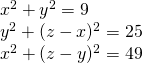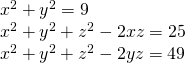Maandelijks archief: oktober 2017

De stellingen van Ceva en Menelaos

Geplaatst op door

Pareltjes uit de oude doos!

De stelling van Ceva zegt : AD, BE en CF snijden elkaar is 1 punt is equivalent met

    \[\dfrac{|AF|}{|FB|}.\dfrac{|BD|}{|DC|}.\dfrac{|CE|}{|EA|}=1\]

Hierbij moeten de verhoudingen opgevat worden als verhoudingen van de overeenkomstige vectoren, zodat de verhouding negatief is als de vectoren tegengesteld zijn. De transversalen AD, BE en CF  worden ook wel Cevianen genoemd. De stelling werd voor het eerst bewezen door Giovanni Ceva in zijn werk De lineis rectis uit 1678. 

Als we stelling van Ceva ‘vertalen’ (  punt wordt lijn en lijn wordt punt, lijn gaat door punt wordt punt ligt op lijn, snijpunt van 2 lijnen wordt verbindingslijnstuk van 2 punten) krijgen we de stelling van Menelaos:

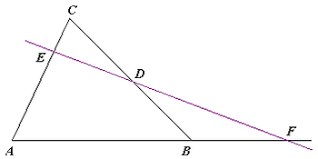
Drie punten, D,E en F, gelegen op de zijden van een driehoek, liggen op één lijn als en slechts als 

    \[\dfrac{|AF|}{|FB|}.\dfrac{|BD|}{|DC|}.\dfrac{|CE|}{|EA|}=-1\]

Merk op dat de verhouding positief is als F tussen A en B ligt, en negatief als F buiten het lijnstuk AB ligt.

 

Gebruik een goede notatie

Geplaatst op door

Het ontbreken van een goede notatie kan de verdere ontwikkeling van een wiskundig begrip tegenhouden. Net zo goed kan een goede notatie  bij het oplossen van een probleem, dit probleem toegankelijker maken en ons naar een goede oplossingsmethode leiden. Het probleem wordt als het ware gecodeerd zodat het veel toegankelijker wordt.

Een voorbeeld:

 

Ik heb 4 kleinkinderen Mirthe (M), Tiebe (T), Joeke (J) en Nienke (N). Op hoeveel manieren kan ik 10 stukken van 2 \euro \ onder hen verdelen?

We kunnen beginnen met een paar voorbeelden:

    \[\begin{array}{c|c|c|c} M&T&J&N\\ \hline xx&xx&xxx&xxx\\ xxxxx&xxxxx&& \end{array}\]

  • Bij de eerste lijn ( xx|xx|xxx|xxx) krijgen Mirthe en Tiebe elk 2 Euro , terwijl Joeke en Nienke elk 3 Euro  krijgen. Op de tweede lijn (xxxxx|xxxxx||) krijgen Mirthe en Tiebe elk 5 Euro en Joeke en Nienke niets.
  • Dus met elke verdeling van de tien munten komt een rijtje van 10 x-en en 3 | en overeen. Dit lijkt een goede notatie voor een verdeling .
  • Omgekeerd komt met elke rij van 10 x-en en 3 | en een verdeling van de 10 stukken van 2 Euro  overeen. Met xxx|xxx|x|xxx geef ik Mirthe, Tiebe en Nienke elk 3 stukken van 2 Euro  en Joeke 1 stuk.
  • Er zijn dus evenveel verdelingen van die 10 muntstukken over mijn kleinkinderen als er dergelijke rijtjes kunnen gevormd worden.
  • Het aantal van dergelijke rijtjes is een herhalingspermutatie van 13 elementen waarvan er 10 van het soort x zijn en 3 van het soort |. Dus zijn er \dfrac{13!}{10!.3!}=260 mogelijke verdelingen.

Het verdelen van de inzet

Geplaatst op door

Een populaire visie op de ontwikkeling van de kanstheorie komt uit de hoek van de kansspelen. Klassiek is het verhaal over Chevalier De Mere ( 1607-1684) die
Pascal ( 1623-1662) vroeg de kans te berekenen om in vier worpen met een dobbelsteen tenminste één zes te gooien.

Een ander mooi voorbeeld vinden we in een werk van Franciscus Van Schooten, uitgegeven in 1660. Daarin staat een bijdrage van Christanus Huygens ( 1629-1695) over Van reckeninghe in Speelen van Geluck. Hierin behandelt hij onder andere het volgend vraagstuk:
Veronderstel dat twee spelers A en B na een gelijke inzet te hebben gegeven het tegen elkaar opnemen in een eerlijk spel. Ze komen overeen dat wie het eerst 6 ronden gewonnen heeft de totale inzet krijgt. Het spel wordt echter afgebroken op het ogenblik dat A 5 spelen gewonnen heeft en B 3 spelen. Hoe moet de inzet redelijkerwijs verdeeld worden?

Cardano (1501-1576) besprak het probleem in 1539 en gaf als oplossing dat speler A dan \dfrac{6}{7} van de pot krijgt en B de rest. Tartaglia ( +-1499-1557) gaf ook een oplossing in 1556 : A krijgt \dfrac{2}{3} van de inzet. Een eerste, naar huidig inzicht, juiste oplossing komt er van Fermat (1601-1665) in een brief van 1654 aan Pascal (1623-1662). Fermat redeneert als volgt: de overeenkomst was wel degelijk 6 rondjes te winnen. Dus moet de inzet verdeeld worden a rato van de winstkansen van beide spelers in de veronderstelling dat het spel wordt uitgespeeld. er kunnen nog hoogstens 3 spelen gespeeld worden die de volgende uitslag kunnen geven ( we schrijven a voor winst voor speler A en b voor winst van speler B): aaa,aab,aba,abb, baa,bab,bba,bbb. Dus 8 mogelijkheden;  in 7 ervan wint speler A en in 1 ervan speler B. Bijgevolg krijgt A uiteindelijk \dfrac{7}{8} van de totale inzet en B slechts \dfrac{1}{8}.

Het mag duidelijk zijn dat het vastleggen van een juiste uitkomstenverzameling hét uitgangspunt moet zijn voor een goede opbouw van het kansexperiment. het was uiteindelijk de Rus Kolmogorov die rond 1930 deze gedachtegang via een axiomatisch systeem goed vastlegde.

Formuleer een eenvoudiger probleem

Geplaatst op door

Om een probleem op te lossen verzamelen we eerst alle gegevens. We proberen ze te begrijpen en te analyseren. Maar soms kunnen we dat niet doen op een betekenisvolle manier omdat de berekeningen te ingewikkeld zijn of omdat er bijvoorbeeld geen speciale gevallen zijn die ons enig inzicht kunnen geven in het probleem. We proberen dan het probleem te herformuleren in een equivalente maar eenvoudiger vorm. Hiervoor zullen we gebruik moeten maken van onze verbeelding en creativiteit. Dikwijls gebruiken we hiervoor algebraïsche of goniometrische formules, substitutie of verandering van onbekende,…

Voorbeeld:

Vind een algemene formule voor de n-de afgeleide van

    \[f(x)=\dfrac{1}{1-x^2}\]

  • f'(x)=\dfrac{2x}{(1-x^2)^2} , f''(x)=\dfrac{2+6x^2}{(1-x^2)^3}, f'''(x)=\dfrac{24x+24x^3}{(1-x^2)^4}. De uitdrukking wordt steeds ingewikkelder en we zien geen regelmaat verschijnen.
  • Misschien kunnen we de opgave eerst vereenvoudigen en dan denken we onmiddellijk aan splitsen in partieelbreuken:

        \[f(x)=\dfrac{1}{2}\Big(\dfrac{1}{1-x}+\dfrac{1}{1+x}\Big)\]

  • Het probleem is nu herleid tot het vinden van een algemene formule voor de n-de afgeleide van g(x)=\dfrac{1}{1-x} en h(x)=\dfrac{1}{1+x}.
  • g'(x)=\dfrac{1}{(1-x)^2}, g''(x)=\dfrac{2}{(1-x)^3}, g'''(x)=\dfrac{2.3}{(1-x)^4}. Zo komen we tot de formule:

        \[g^{n}(x)=\dfrac{n!}{(1-x)^{n+1}}\]

    We kunnen dit eventueel bewijzen via inductie.

  • Analoog vinden we :

        \[h^n(x)=\dfrac{(-1)^n.n!}{(1+x)^{n+1}}\]

  • We besluiten dus:

        \[f^n(x)=\dfrac{n!}{2}\Big(\dfrac{1}{(1-x)^{n+1}}+\dfrac{(-1)^n}{(1+x)^{n+1}}\Big)\]

Opgave 6

Geplaatst op door

Bereken de zijde van het vierkant als je volgende gegevens hebt :
Antwoord

  1. Je hebt 3 inlichtingen, dus als je 3 onbekenden kiest, kan je via een stelsel het probleem misschien oplossen.
  3. Via Pythagoras kunnen we volgende drie vergelijkingen opschrijven:
    x^2+y^2=9\\ y^2+(z-x)^2=25\\x^2+(z-y)^2=49
  4. Uitgerekend geeft dit :
    x^2+y^2=9\\x^2+y^2+z^2-2xz=25\\x^2+y^2+z^2-2yz=49
  5. Uit (1) en (2) volgt z^2-2xz=16 of x=\dfrac{z^2-16}{2z}
  6. Uit (1) en (3) volgt z^2-2yz=40 of y=\dfrac{z^2-40}{2z}
  7. Vullen we nu x en y in bij x^2+y^2=9, dan vinden we dat (z^2-58)(z^2-16)=0.
  8. Hieruit volgt dat de zijde van het vierkant gelijk is aan 4 of \sqrt{ 58}.  Het is duidelijk dat z=4 geen goede oplossing is.