Maandelijks archief: september 2021

Archimedische lichamen

Geplaatst op door

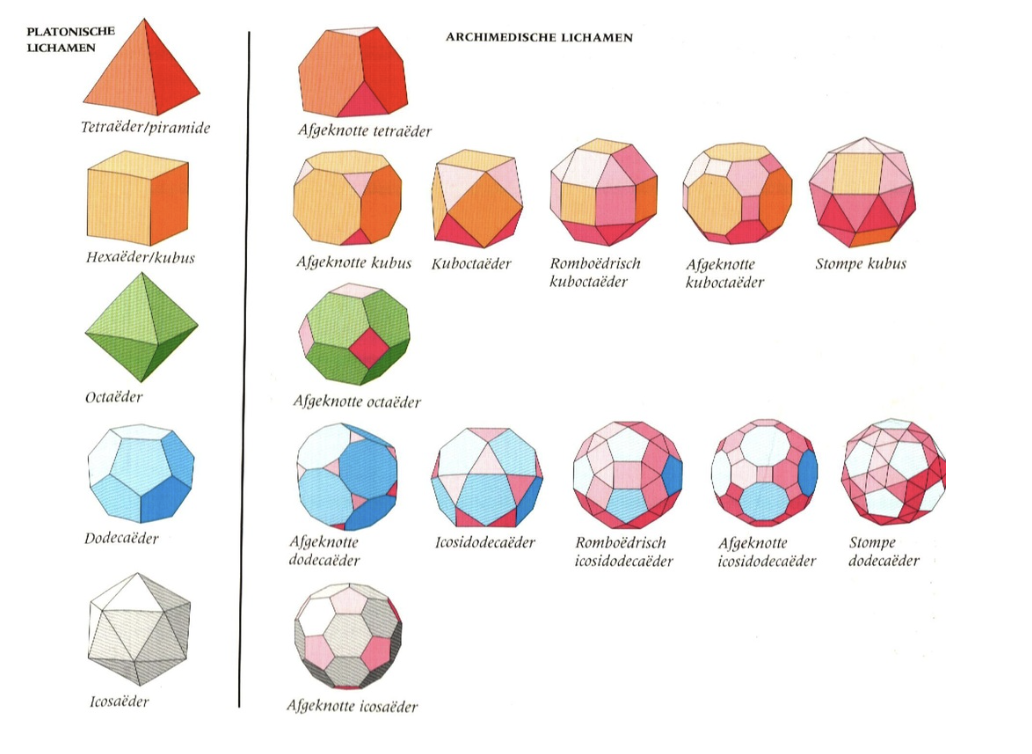
De Platonische lichamen die we zagen zijn regelmatig. Dat wil zeggen dat al hun zijvlakken identiek zijn. De Archimedische lichamen, vernoemd naar Archimedes, zijn half regelmatig, omdat ze twee of meer soorten vlakken hebben.

Alhoewel de Archimedische lichamen verschillende vlakken hebben, zijn hun hoekpunten regelmatig: ze zijn allemaal hetzelfde. Deze vormen zien er vreemder uit en zijn minder bekend, maar als we kijken naar het aantal vlakken, ribben en hoekpunten, zien we de formule terug die we ook bij de Platonische lichamen zagen : V + H – R = 2

Zeven van de Archimedische lichamen zijn gevormd door het afknotten van de platonische lichamen., met andere woorden door de hoeken er af te snijden : 

  • Afgeknotte tetraëder
  • Afgeknotte kubus
  • Afgeknotte octaëder
  • Afgeknotte dodecaëder
  • Afgeknotte icosaëder
  • Afgeknotte kuboctaëder
  • Afgeknotte icosidodecaëder

Drie andere van de Archimedische lichamen zijn gevormd door het uitbreiden van de platonische lichamen. 

  • Icosidodecaëder
  • Romboëdrische icosidodecaëder
  • Kuboctaëder

De twee laatste  Archimedische lichamen zijn gevormd door de vlakken van een kubus en een dodecaëder naar buiten te bewegen, zodat elk vlak een draai krijgt. Bij de stompe Archimedische lichamen wordt elke veelhoek omringd door gelijkzijdige driehoeken.

  • Stompe kubus
  • Stompe dodecaëder

Griekse wiskunde deel 7

Geplaatst op door

Archimedes leefde in Syracuse van 287 tot. 212 v.C. en verbleef aan het hof van koning Hieron. Bij zijn tijdgenoten verwierf hij grote vermaardheid, niet zozeer voor zijn zuiver wetenschappelijk werk, maar vooral door zijn talrijke technische realisaties van ingenieuze werktuigen en machines( pompen, kranen , katapulten,..).

Als zuiver platonische wiskundige is hij zelf minder gelukkig met zijn materialistische nevenactiviteiten. Tijdens een reis naar Egypte maakt hij kennis met Euclides en vanaf dan onderhoudt hij een vrij drukke wetenschappelijke briefwisseling met andere wiskundigen zoals bvb. Erastosthenes. Meestal deelt hij enkel resultaten mee, daarmee zijn collega’s uitdagend om er zelf een bewijs voor te vinden.

Van zijn uitgebreid oeuvre bleven enkel volgende werken bewaard: Over het evenwicht van vlakke figuren en hun zwaartepunt,  de kwadratuur van de parabool, de methode, over de bol en de cilinder, over de conoïden en de sferoïden. over de spiralen, over de drijvende lichamen, de cirkelmeting en de zandrekenaar.

De methode: dit werk werd pas in 1906 bij toeval teruggevonden door de Deense filoloog Heiberg op een palimpsest uit een kloosterbibliotheek. In dit werk leert Archimedes ons dat de strenge deductieve methode , waarvan Aristoteles de formele regels vastlegde en die Euclides in zijn Elementen zo perfect illustreerde, een procédé is dat haast alleen nuttig is om bewijzen van gekende resultaten te leveren.Voor het creatief onderzoekingswerk geeft hij de voorkeur aan zogenaamde mechanische methodes die, omdat ze op fysische inzichten berusten, minder streng maar zoveel vruchtbaarder zijn. Nadat hij langs deze heuristische weg resultaten ontdekt heeft, geeft hij een streng bewijs waarbij hij dikwijls gebruik maakt van Eudoxos’ exhaustiemethode.

Lissajous figuren

Geplaatst op door

Op de grens van wiskunde en kunst vind je figuren als

We noemen het Lissajous figuren naar de Franse wiskundige Jules Antoine  Lissajous( 1822- 1880). Gefascineerd door trillingen, deed hij baanbrekend werk op het gebied van akoestiek en optica.

Een Lissajous figuur wordt verkregen door de parameter vergelijkingen:

    \[x=A \sin (at+c)\]

    \[y=B\sin bt\]

 

c noemt men het faseverschil. In onderstaande tabel zie je bovenaan verschillende waarden van c

 

Een aantal grafieken met bijhorende waarden van a en b


Een paar andere grafieken (soms in 3D):

 

Hoe lang zal de wereld bestaan?

Geplaatst op door

In de grote tempel van Benares, onder de koepel die het centrum van de wereld aangeeft, staat een grote bronzen plaat, waarin drie diaman­ten naalden zijn bevestigd, elk ter lengte van een onderarm en zo dik als het lichaam van een bij.
Op één van deze naalden plaatste God bij de Schepping vierenzestig schijven van zuiver goud. De grootste rustte op de bronzen plaat, de volgende werden naar boven toe steeds kleiner. Dit is de toren van Brahma.

Dag en nacht, zonder onderbreking, verplaatsen de priesters de schijven van de ene naald naar de andere, overeenkomstig de vaste en onveranderlijke wetten van Brahma, volgens welke de dienstdoende priesters niet meer dan één schijf tegelijk mogen bewegen en geen schijf geplaatst mag worden op een naald die al een kleinere schijf bevat. Als de vierenzestig schijven van de naald waarop God ze bij de Schepping plaatste, overgebracht zullen zijn naar één van de andere, dan zullen de torens en de tempel en de priesters tegelijk tot stof vervallen en met een donderslag zal de wereld vergaan.”

Hoe lang moeten de priesters werken, als ze zonder ooit een fout te maken elke seconde één schijf overbrengen?

Je kan dit proces heel gemakkelijk recursief beschrijven:  Met n schijven: los het probleem op door de bovenste n-1 schijven naar pin B te brengen, met pin C als hulppin. Vervolgens wordt -n-de schijf naar pin C gebracht. Tot slot worden de eerste n-1   schijven van pin B naar pin C gebracht, met pin A als hulppin. Als we met u_n het aantal zetten noteren om n schijven van één pin naar een andere te zetten , dan geldt:

    \[u_n=2u_{n-1}+1\]

We kunnen dit omzetten naar het expliciet voorschrift u_n=2^n-1. De wereld zal dus 2^{64}-1 jaren bestaan, dat is zo ongeveer duizend miljard jaar. Als het verhaal klopt natuurlijk….

Als spel werd dit onder de naam Torens van Hanoi op de markt gebracht in 1863 door Edouard Lucas, onder de schuilnaam prof Claus.

Delen in Python

Geplaatst op door

Een deling in Python:

  • In de verzameling der reeële getallen in [1]
  • In de verzameling van de gehele getallen in [2], kan je quotiënt en rest bepalen bij deling van a door b
    Een mooie toepassing is van een reeks getallen nakijken of ze even zijn of niet. Even getallen geven rest 0 bij deling door 2: