Maandelijks archief: augustus 2021

Punt van Torricelli

Geplaatst op door

Zoek binnen een driehoek een punt T zodat de som van de afstanden van T tot de hoekpunten zo klein mogelijk is. Deze vraag werd door Fermat voorgelegd aan Evangelista Torricelli (1608-1647) en was bedoeld als een soort uitdaging. Vandaar dat men dit punt het punt van Torricelli of het punt van Fermat noemt. Torricelli was assistent van Galilei en volgde hem op als wiskundige aan het hof van groothertog van Toscane.

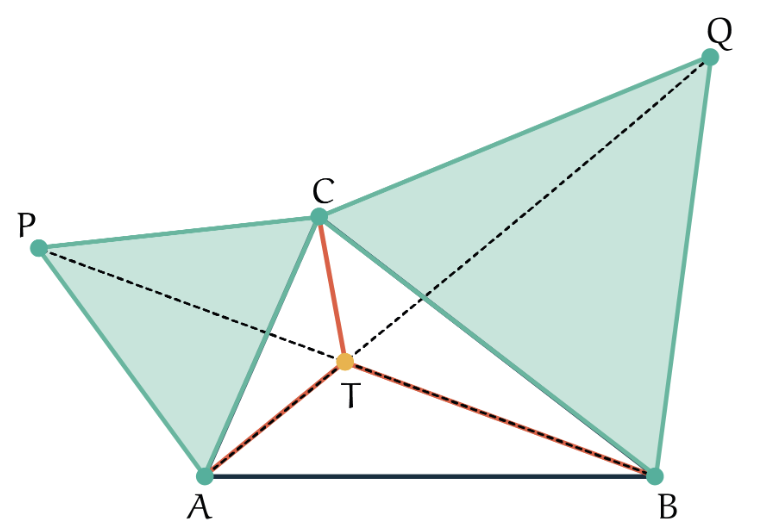
Hierboven zie je de constructie: construeer op twee zijden van de gegeven driehoek ABC gelijkzijdige driehoeken PAC en BCQ. Verbind Q met A en P met B. Het snijpunt van BP en AQ geeft het punt T. 

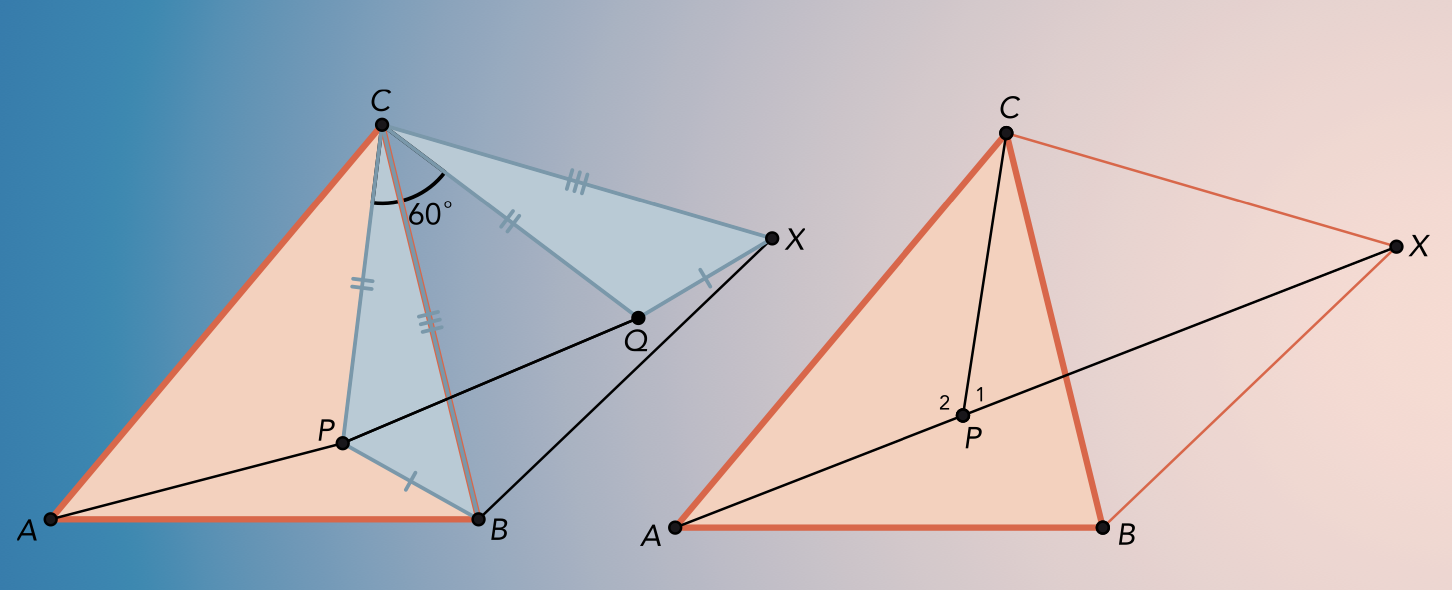
Om dit probleem te kraken, gebruiken we de driehoeksongelijkheid. Die zegt dat de kortste weg tussen twee punten de rechte lijn is door die punten. Neem nu een willekeurig punt P binnen de driehoek. en draai de driehoek CPB 60^\circ rond C zodat  P op Q en B op X wordt afgebeeld ( zie linker figuur). De driehoeken CPB en CQX zijn dan congruent en dus is |PB|=|QX| en |PC|=|CQ|. Maar dan is driehoek CPQ gelijkzijdig en is |PC|=|PQ|. Dan is de som S van de afstanden van P tot de hoekpunten van de gegeven driehoek gegeven door S=|AP|+|PQ|+|QX|. Volgens de driehoeksongelijkheid wordt S dan minimaal als A,P,Q en X op 1 lijn liggen. De positie van X hangt niet af van de keuze van P, dus moeten we P  zo kiezen dan A,P,Q en X op 1 lijn liggen. Uit de tekening is het duidelijk dat we P zo moet kiezen dat P op AX ligt en de hoek tussen CP en PX moet 60^\circ zijn. Dit komt neer op de constructie die hierboven werd uitgelegd.

Merk ook op dat de lijnstukken vanuit het punt van Torricelli T, naar de hoekpunten toe, onderling hoeken maken die allemaal gelijk zijn aan  120^\circ.

 

Een opgave over absolute waarden

Geplaatst op door

Schrijf een Python programma dat de absolute waarde van een getal uit een gegeven lijst afdrukt als het getal kleiner is dan -5 of groter dan 2. Zoniet wordt er gewoon afgedrukt dat het getal niet werd uitgevoerd.

Spoiler

 

 

  • We gaan met een for lus alle getallen uit de gegeven lijst controleren.
  • Als het voldoet aan de voorwaarde <-5 of >2 dab drukken we de absolute waarde af ( Abs(x)).
  • Zoniet geven we de andere boodschap.

 

merk op dat er 3 manieren gegeven zijn om tekst in te voegen. De eerste via een commentaar lijn ( #…). En dan 2 mogelijkheden met een print bevel.

 

Griekse wiskunde deel 6

Geplaatst op door

Over de mens Euclides is weinig bekend, We weten dat hij rond 300 v.C. wiskunde doceerde in het museion van Alexandrië. Gevormd in de scholen van Plato en Aristoteles, is hij dus één van de Griekse intellectuelen die naar Alexandrië toestroomden om er beroepsgeleerde te worden. 

Uit de analyse van zijn werken is vrij duidelijk te zien dat Euclides geen groot wiskundige was, maar wel een buitengewone didacticus. Zo ligt het geniale van zijn Elementen niet zozeer in de inhoud, want die is afkomstig van zijn grote voorgangers Archytas, Theatetus en Eudoxos. Maar het bijzondere is de gepaste keuze van de volgorde, waar de verschillende onderdelen worden behandeld. Een vrij omvangrijk eerste deel is ook toegankelijk voor middelmatige leerlingen, de moeilijke delen komen pas later aan de beurt.

De elementen staat zeker op de lijst van de boeken die het grootst aantal uitgaven en vertalingen hebben gekend. Deze bestseller omvat 13 boeken, waaraan door latere wiskundigen nog 2 boeken zijn toegevoegd. ( o.a. een boek over regelmatige veelvlakken). De boeken 1 tot 4 handelen over de meetkunde van de rechte, de driehoek en de cirkel. Boeken 5 en 6 zijn gewijd aan de leer van de evenredigheden en de gelijkvormige figuren. In boeken 7,8 en 9 gaat het over de natuurlijke getallen. Boek 10 bestudeert de irrationale getallen. Tenslotte gaat het in de boeken 11,12 en 13 over de meetkunde van de ruimte en de 5 regelmatige veelvlakken.

De gewichten van Bachet

Geplaatst op door

Dit probleem werd 400 jaar geleden aangekaart door de Franse wiskundige Claude Gaspard Bachet de Méziriac(1581-1638): wat is de kleinst mogelijke verzameling gewichten waarmee je iedere gehele kilo van 1 tot 40 kan afwegen?

Eigenlijk staat dit raadsel in het liber Abaci van Leonardo Pisano(1202). Bachet was een dichter, vertaler en tolk en was de schrijven van het raadselboek Problèmes plaisants et délectable qui se font par les mombers(1612). In dit standaardwerk voor creatieve wiskunde staat onder andere dit probleem.

Elk natuurlijk getal tussen 1 en 40 kan je in het drietallig talstelsel schrijven. Daarvoor heb je enkel de getallen 1,3,9 en 27 nodig. Dit zijn onze basisgewichten. Maar hoe kunnen we dan alle gewichten tussen 1 en 40 afwegen?

  • In de drietallige schrijfwijze komen alleen nullen en enen voor: neem bvb. 13=(111)_3=1+3+9. Dus kan je met de gewichten 1,3,9 een gewicht van 13 afwegen.
  • Wat te doen als er een 2 voorkomt in de drietallige schrijfwijze? Neem bvb. (121)_3=1+2*3+9=1+(3-1)*3+9=1-3+2*9=1-3+(3-1)9=1-3-9+27=16  Je kan dit dan schrijven als 1+27 = 16 +3 +9. Leg dan de gewichten 1 en 27 op de linker schaal en de gewichten 3,9 samen met het gewicht 16 op de rechterschaal.
  • Omdat de som van 1,3,9 en 27 juist 40 is kan je dus zo elk gewicht tussen 1 en 40 afwegen!

Een getal raden

Geplaatst op door

Je mag  een getal kiezen  uit de verzameling {0,1,2,…,15}. Hoe kan ik met een minimum aantal ja/neen vragen dit getal raden?

Antwoord

 

 

  • Een eerste mogelijk is te werken via de binaire schrijfwijze van het getal. Elk getal uit de gegeven verzameling heeft een unieke schrijfwijze met 4 nullen of enen in het tweetallig stelsel. Je n-de vraag is dan : is het n-de cijfer een 0 of een 1 (met n=1,2,3 of 4).
  • Met minder vragen lukt het niet want met 3 vragen kan je slechts 8 verschillende ja/neen antwoorden krijgen.
  • Een tweede mogelijkheid is werken met intervallen. Je vraagt eerst of het getal kleiner is dan 8. Is het antwoord ja dan deel je het interval terug is twee en vraagt of het getal kleiner is dan 4. was het antwoord op de eerste vraag neen, dan vraag je of het getal kleiner is dan 12. na vier vragen ( telkens het interval halveren) kom je bij een unieke oplossing.