Een kaart van de route uit toerisme Vlaanderen, Westtoer: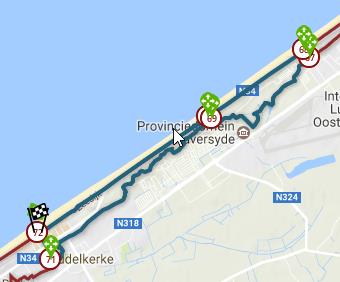

Omdat 7 een priemgetal is , zal er maar 1 groep zijn van orde 7, namelijk de cyclische groep ![]() van orde 7. Er zijn niet-triviale eenheden in
van orde 7. Er zijn niet-triviale eenheden in ![]() . meer hierover in volgende tekst.
. meer hierover in volgende tekst.
De Franse wiskundige B.Pascal legde omstreeks 1650 samen met Pierre de Fermat de grondslagen voor de kansrekening. Het berekenen van winstkansen is echter niet zo eenvoudig en je komt bij de toepassingen verschillende schijnbare tegenstellingen tegen.
Deze paradox is genoemd naar de statisticus E.H.Simpson en werd in 1951 voor het eerst gepubliceerd. Laten we die paradox bespreken aan de hand van een voorbeeld.
In bovenstaande tabel staan de slaagcijfers van jongens en meisjes voor 3 studierichtingen: medische, humane en exacte wetenschappen. Uit deze tabel blijkt dat in de 3 verschillende richtingen de slaagpercentages van de meisjes net iets hoger liggen dan bij de jongens. Paradoxaal genoeg blijken de jongens in het totaal toch beter te presteren dan de meisjes: 51% tegen 46%.
De verklaring is dat meisjes zich meestal inschreven voor studierichtingen waar de slaagkansen kleiner waren. Dit is Simpsons paradox: als je gegevens van twee groepen op een onhandige manier combineert, dan lijken de resultaten van de groepen om te draaien.
In essentie betekent deze methode niet meer of minder dan het bekijken van de meest extreme situatie die zich kan voordoen of zou moeten kunnen voordoen. Als je ooit om een of andere reden het niet bestaan van bepaalde objecten wil aantonen, bijvoorbeeld van het maximum van een verzameling, zal deze techniek zeker een nuttig hulpmiddel zijn. Je bepaalt een verzameling objecten en selecteert een object waarbij een bepaalde eigenschap minimaal of maximaal is. Werk verder tot je een tegenspraak krijgt.
Bekijken we eens een voorbeeld: In een groep van n personen zijn er steeds twee die binnen deze groep evenveel vrienden hebben. We veronderstellen dat vriendschap wederzijds is.
Veronderstel dat ze allemaal een verschillend aantal vrienden hebben. Vermits er ![]() personen zijn en omdat iemand maximaal
personen zijn en omdat iemand maximaal ![]() vrienden kan hebben, hebben die n personen respectievelijk
vrienden kan hebben, hebben die n personen respectievelijk ![]() vrienden. Bekijken we het extreme geval dat iemand dus
vrienden. Bekijken we het extreme geval dat iemand dus ![]() vrienden heeft. Met andere woorden hij is met iedereen bevriend. Maar omdat vriendschap wederzijds is, heeft iedereen dus minstens 1 vriend. Bijgevolg is er niemand met 0 vrienden. Dit geeft onze tegenpraak en bijgevolg zijn er minstens twee personen met evenveel vrienden.
vrienden heeft. Met andere woorden hij is met iedereen bevriend. Maar omdat vriendschap wederzijds is, heeft iedereen dus minstens 1 vriend. Bijgevolg is er niemand met 0 vrienden. Dit geeft onze tegenpraak en bijgevolg zijn er minstens twee personen met evenveel vrienden.
Sommige stellingen zijn zo eenvoudig en elegant dat je jezelf kan afvragen: Waarom ben ik daar niet zelf op gekomen? Dit geldt onder andere voor de volgende stelling die vernoemd wordt naar zijn ontdekker: de Oostenrijkse wiskundige Georg Alexander Pick, geboren in 1859 in Wenen en overleden in 1942 in het concentratiekamp Theresienstadt.
Het gaat over de oppervlakte van een roosterveelhoek, dit wil zeggen een veelhoek waarvan de hoekpunten op de punten van een regelmatig vierkant rooster liggen. Noteer met ![]() het aantal roosterpunten op de rand van de veelhoek V en met
het aantal roosterpunten op de rand van de veelhoek V en met ![]() het aantal roosterpunten in het inwendige van V.
het aantal roosterpunten in het inwendige van V.
![]()
Voor deze veelhoek is de oppervlakte dus ![]() oppervlakte eenheden.
oppervlakte eenheden.