Gelijkaardig aan de rij van Fibonacci, kunnen we ook de rij van Padovan definiëren, als de rij met 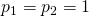 en
en
![Rendered by QuickLaTeX.com \[p_n=p_{n-2}+p_{n-3}\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-d9e38493e4e75e365eee291b46f3428c_l3.png)
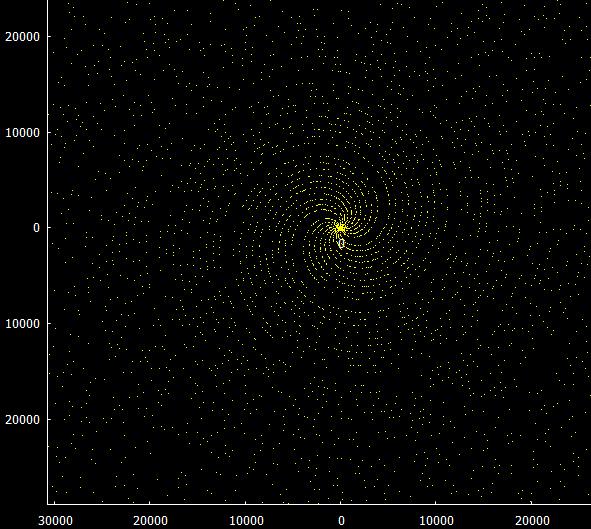
De rij van Padovan is vernoemd naar de schrijver en architect Richard Padovan die zijn ontdekking toegeschreef aan de Nederlandse architect Hans van der Laan . Hieronder zie je een spiraal van gelijkzijdige driehoeken waarvan de lengten der zijden gelijk zijn aan de de getallen uit de rij van Padovan.
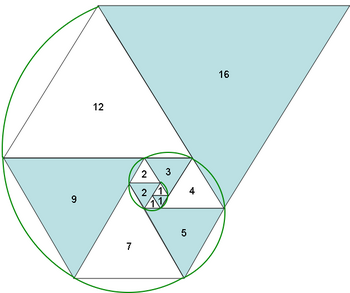
Als we de rij bestuderen van de quotiënten van twee opeenvolgende getallen uit de rij van Padovan, bekomen we volgende rij : 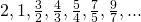 . We vermoeden dat deze rij convergeert naar een limiet L.
. We vermoeden dat deze rij convergeert naar een limiet L.
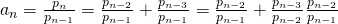 . Dus is
. Dus is 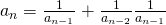 . In de limiet wordt dit
. In de limiet wordt dit 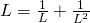 . Bijgevolg voldoet de limiet L aan de betrekking
. Bijgevolg voldoet de limiet L aan de betrekking
![Rendered by QuickLaTeX.com \[L^3-L-1=0\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-33801dd56c993b87b104608edca68e93_l3.png)
Zo vinden we voor L de benaderende waarde
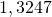
.
Dit getal noemen we het plastisch getal. Het plastisch getal heeft met de gulden snede nog meer eigenschappen gemeen, maar sommigen gaan nog verder en dichten aan deze getallen verregaande eigenschappen toe omtrent schoonheid.
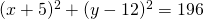 . Bepaal de minimumwaarde van
. Bepaal de minimumwaarde van 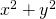 .
.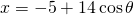 en
en 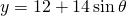 . Dit invullen in
. Dit invullen in 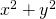 geeft een functie in één variabele :
geeft een functie in één variabele : 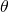 . Via de theorie van afgeleiden kan je dan de minimale waarde vinden.
. Via de theorie van afgeleiden kan je dan de minimale waarde vinden.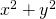 gelijk zijn aan 1.
gelijk zijn aan 1.