De Midden-Europese Wiskunde Olympiade (MEMO) is een jaarlijkse terugkerende wiskundige wedstrijd die voor het eerst werd gehouden in 2007. Het is de opvolger van de Oostenrijkse-Poolse Wiskunde Competitie die 29 keer gehouden werd tussen 1978 en 2006 tussen één Oostenrijkse en één Pools team. De eerste MEMO vond plaats in Eisenstadt in Oostenrijk.
Nu nemen tien landen deel aan de MEMO: Oostenrijk, Kroatië, Tsjechië, Duitsland, Hongarije, Litouwen, Polen, Slowakije, Slovenië en Zwitserland.

Net als bij de Internationale Wiskunde Olympiade (IMO),participeert elk land met maximaal zes studenten en twee teamleiders. Eén van de belangrijkste doelstellingen van de nieuwe wedstrijd was de mogelijkheid te scheppen voor een groter aantal studenten om ervaring in internationale wedstrijden op te doen. De teams die deelnemen aan het MEMO zijn typisch disjunct van de IMO teams van hun land. Ook wordt MEMO bedoeld om jongere studenten voor een toekomstige deelname aan de Internationale Wiskunde Olympiade voor te bereiden.
De MEMO bestaan uit een individuele wedstrijd en een team competitie met een duur van vijf uur. De problemen zijn gewoonlijk verdeeld over vier gebieden: algebra, combinatoriek, meetkunde en getaltheorie. In de individuele wedstrijd, lossen de leerlingen een probleem op uit elk gebied. De competitie team bestaat uit acht problemen, twee uit elk gebied (hoewel bij de eerste twee MEMO’s ook het team competitie slechts vier problemen had ). In de teamcompetitie lossen de studenten van elk team samen de problemen op en dat geeft de competitie een heel bijzondere sfeer. Het team deel van de competitie bestond ook bij de Oostenrijk-Poolse wiskunde competitie, maar is eerder een zeldzaamheid in het landschap van wiskundige wedstrijden.
![]() oplossen. De meest wiskundige manier is op zoek gaan naar een primitieve functie F(x) van f(x) en dan is
oplossen. De meest wiskundige manier is op zoek gaan naar een primitieve functie F(x) van f(x) en dan is ![]() . Maar soms is het berekenen van een primitieve functie een zeer lastige of onmogelijke taak. Is het in die gevallen dan onmogelijk om de bepaalde integraal te berekenen?
. Maar soms is het berekenen van een primitieve functie een zeer lastige of onmogelijke taak. Is het in die gevallen dan onmogelijk om de bepaalde integraal te berekenen?![]() te benaderen:
te benaderen:![Rendered by QuickLaTeX.com [a,b]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-611c86eb16b0fb9954e2532a2f68b269_l3.png) in een even ,n , aantal stukken en stel
in een even ,n , aantal stukken en stel 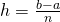 .
.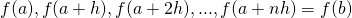 .
.![Rendered by QuickLaTeX.com \int_a^b f(x)\ dx \approx \frac{h}{3}\Big [ f(a)+f(b)+4\Big(f(a+h)+f(a+3h)+\cdots+f(a+(n-1)h\Big)+2\Big(f(a+2h)+f(a+4h)+\cdots+f(a+(n-2)h)\Big)\Big]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-f59df2699267624b400f73f5e7ba56e1_l3.png)
![]() over
over ![]() te benaderen door de oppervlakte onder een parabool door de punten
te benaderen door de oppervlakte onder een parabool door de punten ![]() ,
,![]() en
en ![]() .
.![]()
![]() , dan us
, dan us ![]() en kunnen we de bepaalde integraal benaderen door
en kunnen we de bepaalde integraal benaderen door ![]()