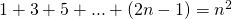Nootje 62

Geplaatst op 2 oktober 2025 door admin

$f(1)=0$ en $f(x)=x+f(x-1) ,x \in \mathbb{N}$ . Bereken $f(100)$ .

“Antwoord”

We weten dat $f(x)-f(x-1)=x$ voor alle natuurlijke getallen x. We schrijven deze formule op voor x van 1 tot n:
$f(1)-f(0)=1$ .
$f(2)-f(1)=2$ .
$f(3)-f(2)=3$ .
…
$f(n)-f(n-1)=n$ .
Als we alles bij elkaar optellen, zien we in het linkerlid bijna alle termen tegen elkaar wegvallen en we behouden $f(n)-f(0)=1+2+3+...+n$ .
Nu is $f(0)=1$ en de som in het rechterlid is $\frac{1}{2}n(n+1)$ .
Bijgevolg is $f(n)=\frac{1}{2}n(n+1)+1$ en
$f(100)=\frac{1}{2}100.101 +1=5051$

Sommen van machten

Geplaatst op 14 september 2025 door admin

We kennen allemaal het verhaal van Gauss om de som van de eerste n natuurlijke getallen te berekenen. Gauss berekende deze som door de reeks in paren te verdelen en te bedenken dat elk paar dezelfde som heeft, wat een efficiënte manier bood om de totale som snel te vinden.

In bijgevoegde tekst gaan we op zoek naar een algemenere methode waarbij we ook de som kunnen berekenen van de n natuurlijke tweede, derde , vierde en vijfde machten .

Rekenkundige rijen

Geplaatst op 22 oktober 2015 door admin

Een rekenkundige rij (RR) $u_n$ is een rij van getallen zodat het verschil van twee opeenvolgende termen van die rij constant is. Deze constante noemt men het verschil v van de rij.

De algemene term van de rij is $u_n=u_1+(n-1)v$
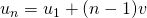
De som van n termen van een RR wordt gegeven door :
$u_1+u_2+\cdots+u_n=\dfrac{u_1+u_n}{2} .n$
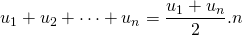
Meer speciaal is $1+2+3+...+n=\dfrac{n(n+1)}{2}$
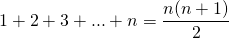
Ook is $1+3+5+...+(2n-1)=n^2$

Wiskunde is leuk

Tag archieven: som eerste n natuurlijke getallen

Nootje 62

$f(1)=0$ en $f(x)=x+f(x-1) ,x \in \mathbb{N}$ . Bereken $f(100)$ .

Sommen van machten

Rekenkundige rijen

en . Bereken .

$f(1)=0$ en $f(x)=x+f(x-1) ,x \in \mathbb{N}$ . Bereken $f(100)$ .