Tag archieven: leuke wiskunde

Hoger Lager

Geplaatst op door

Men neemt de 10 speelkaarten van de aas tot en met de tien van een bepaalde kleur. De speler zet een bepaald bedrag in. Daarna worden de kaarten geschud en de speler legt ze één na één met de beeldzijde op tafel. Telkens als de neergelegde kaart een hogere waarde heeft dan alle voorgaande kaarten, wint de speler een vast bedrag. Bereken de kans op winst bij de k-de kaart en wat is de gemiddelde winst per spel?

Veronderstel dat het spel gespeeld wordt met zelfgemaakte kaartjes die genummerd zijn van 1 to en met n. De kans op succes met het k-de kaartje noteren we met p_k.

Om deze kans te berekenen, zoeken we eerst het aantal manieren waarop de eerste k kaarten kunnen worden neergelegd. Dit is gelijk aanzet aantal k-variaties van n , genoteerd met V(n,k). We weten dat

    \[V(n,k)=\dfrac{n!}{(n-k)!}\]

Daarna berekenen we het aantal mogelijkheden waarbij de k-de kaart succes geeft. Dit hangt af van de waarde w_k van de k-de kaart. Immers:

  • Als 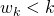w_k<k, dan is het onmogelijk dat de k-de kaart hoger is dan alle vorige kaarten.
  • Als 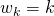w_k=k, dan win je als de vorige 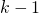k-1 kaarten de nummers 1 tot en met 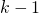k-1 zijn. Zo zijn er 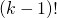(k-1)! mogelijkheden.
  • Als 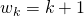w_k=k+1, dan heb je succes als de vorige 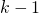k-1 kaarten een nummer hebben van 1 tot en met k. Hiervan zijn er 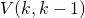V(k,k-1) mogelijkheden.
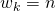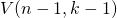  • We kunnen zo verder werken en vinden dat als w_k=n er V(n-1,k-1) winstmogelijkheden zijn.

Het totaal aantal gunstige mogelijkheden is dan V(k-1,k-1)+V(k,k-1)+...+V(n-1,k-1). Via inductie kan men aantonen dat deze som gelijk is aan

    \[\dfrac{n!}{k(n-k)!}\]

Het is tenslotte niet moeilijk om de kans op succes met de k-de kaart uit te rekenen. Gebruik makend van de formule van Laplace vinden we

    \[p_k=\dfrac{1}{k}\]

We merken onmiddellijk op dat dit resultaat totaal niet afhangt van het aantal kaarten waarmee het spel gespeeld wordt. Stel nu even dat je bij winst bij de k-de kaart telkens een bedrag b krijgt.  Als X de winst is per spelletje  met n kaarten, dan is de gemiddelde winst gegeven door

    \[E(X)=\sum_{k=1}^{k=n}b.\dfrac{1}{k}\]

Bij een uitkering van 5 Euro per gewonnen kaart, vind je :

n=5   E(X)=11,4
n=10   E(X)=11,6
n=15   E(X)=16,6
n=20   E(X)=18

 

 

Nootje 13

Geplaatst op door

De zijden van de driehoek ABC hebben gehele getallen als lengte en de omtrek is 7. Bepaal alle mogelijke lengtes van zijde AB.

Antwoord

  • Volgens de driehoeksongelijkheid is de grootst mogelijke zijde 3. Want stel dat het 4 zou zijn dan blijft er nog voor de som van de andere zijden 3 over en omdat elke zijde kleiner is dan de som van de andere twee, kan dat niet
  • Ze kunnen ook niet alle drie een lengte kleiner dan 3 hebben omdat de omtrek anders nooit 7 kan zijn.
  • Er is dus een zijde met lengte 3. Voor de andere zijden heb je dan 2 en 2 of 1 en 3.
  • Bijgevolg kan AB lengte 1,2 of 3 hebben.